
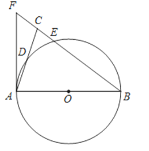
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
【答案】(1)证明见解析;(2)CE=2,AF=![]()
【解析】
(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)首先连接AE,设CE=x,由勾股定理可得方程:(2![]() )2=x2+(3x)2 .然后由tan∠ABF=
)2=x2+(3x)2 .然后由tan∠ABF=![]() ,求得答案.
,求得答案.
(1)证明:如图,连接BD.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°.
∵AF是⊙O的切线,
∴∠FAB=90°,
即∠DAB+∠CAF=90°.
∴∠CAF=∠ABD.
∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.
∴∠ABC=2∠CAF.
(2)解:如图,连接AE.
∴∠AEB=90°.
设CE=x,
∵CE:EB=1:4,
∴EB=4x,BA=BC=5x,AE=3x.
在Rt△ACE中,AC2=CE2+AE2 .
即(2![]() )2=x2+(3x)2 .
)2=x2+(3x)2 .
∴x=2.
∴CE=2,
∴EB=8,BA=BC=10,AE=6.
∵tan∠ABF=![]() .
.
∴![]() .
.
∴AF=![]() .
.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
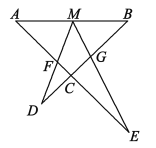
【题目】如图,点M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于点F,ME交BC于点G.写出图中的所有相似三角形,并选择一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
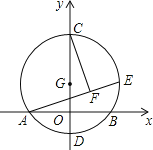
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府在广场上树立了如图所示的宣传牌,数学兴趣小组的同学想利用所学的知识测量宣传牌的高度AB,在D处测得点A、B的仰角分别为38°、21°,已知CD=20m,点A、B、C在一条直线上,AC⊥DC,求宣传牌的高度AB(sin21°≈0.36,cos21°≈0.93,tan21°≈0.38,sin38°≈0.62,cos38°≈0.78,tan38°≈0.79,结果精确到1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
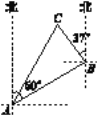
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A′在Rt△ABC的边AB上,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,A'B'与BC交于点D,连接BB′,求线段BB′的长度.
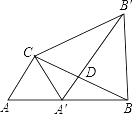
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D,交BC于点E,连接BD.
(1)线段BD与ID相等吗?证明你的结论.
(2)证明:ID2=DEAD.
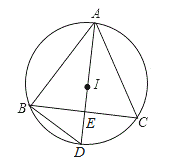
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com