
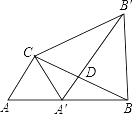
【题目】如图,点A′在Rt△ABC的边AB上,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,A'B'与BC交于点D,连接BB′,求线段BB′的长度.
【答案】2![]()
【解析】
先根据直角三角形的性质求出BC、AB的长,再根据图形旋转的性质得出AC=A′C,BC=B′C,再由A′B=A′C即可得出∠A′CB=30°,故可得出∠BCB′=60°,进而判断出△BCB′是等边三角形,故可得出结论.
解:∵Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,
∴BC= ![]() =2
=2 ![]() ,
,
∵∠A=60°,
∴△AA′C是等边三角形,
∴AA′= ![]() AB=2,
AB=2,
∴A′C=A′B,
∴∠A′CB=∠A′BC=30°,
∵△A′B′C是△ABC旋转而成,
∴∠A′CB′=90°,BC=B′C,
∴∠B′CB=90°﹣30°=60°,
∴△BCB′是等边三角形,
∴BB′=BC=2![]() .
.


科目:初中数学 来源: 题型:
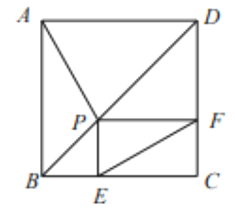
【题目】如图,己知正方形ABCD的边长为4, P是对角线BD上一点,PE⊥BC于点E, PF⊥CD于点F,连接AP, EF.给出下列结论:①PD=![]() EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为
EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为![]() ;⑥AP⊥EF.其中正确结论的序号为( )
;⑥AP⊥EF.其中正确结论的序号为( )
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
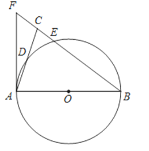
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
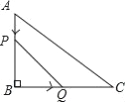
【题目】如图,在△ABC中,∠B=90°,BC=8 AB=6cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张正面分别标有数字![]() 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为![]() ,另有一个被均匀分成4份的转盘,上面分别标有数字
,另有一个被均匀分成4份的转盘,上面分别标有数字![]() ,转动转盘,指针所指的数字记为
,转动转盘,指针所指的数字记为![]() (若指针指在分割线上则重新转一次),则点
(若指针指在分割线上则重新转一次),则点![]() 落在抛物线
落在抛物线![]() 与
与![]() 轴所围成的区域内(不含边界)的概率是__________.
轴所围成的区域内(不含边界)的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是两根木棒及其影子的情形.

(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com