
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD=1,将△ACD沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则PB+PE的最小值是________.

科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,装有红球、白球、黄球共12个,这些球除颜色外完全相同,
从中随机摸出一个球,则:
(1)若盒子中有红球3个,则摸到红球的概率为_________;
(2)若摸到黄球的概率为![]() ,则该盒子中装有黄球的个数是__________个;
,则该盒子中装有黄球的个数是__________个;
(3)若将这12个球分别标上1至12这十二个数字,则摸到的数字是0的概率为________;摸到的数字是偶数的概率为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在街头巷尾会遇到一类“摸球游戏”,摊主把分别标有数字1,2,3的3个白球和标有数字4,5,6的3个黑球放在口袋里![]() 球除颜色外,其他均相同
球除颜色外,其他均相同![]() ,让你摸球
,让你摸球![]() 规定:每付3元钱就玩一局,每局连续摸两次,每次只能摸一个,第一次摸完后把球放回口袋里搅匀后再摸一次,若前后两次摸得的都是白球,摊主就送你10元钱的奖品.
规定:每付3元钱就玩一局,每局连续摸两次,每次只能摸一个,第一次摸完后把球放回口袋里搅匀后再摸一次,若前后两次摸得的都是白球,摊主就送你10元钱的奖品.
![]() 用列表法或树状图表示摸出的两个球可能出现的所有结果;
用列表法或树状图表示摸出的两个球可能出现的所有结果;
![]() 求获奖的概率.
求获奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
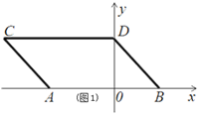
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0).且a,b满足![]() +(a-2b+7)2=0.现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
+(a-2b+7)2=0.现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)请直接写出A,B两点的坐标.
(2)如图,点P是线段AC上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段AC上移动 时(不与A,C重合),请找出∠PQD,∠OPQ,∠POB的数量关系,并证明你的结论.
(3)在坐标轴上是否存在点M,使三角形MAD的面积与三角形ACD的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做投掷骰子(质地均匀的正方体)实验,共做了50次试验,将记录的数据进行整理,绘制了如下的统计表:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 8 |
| 9 | 9 | 7 |
频率 | 0.14 |
| 0.20 | 0.18 | 0.18 | 0.14 |
(1)上表中,![]() =______,
=______,![]() =_______.
=_______.
(2)正在做掷骰子实验的小颖和小明准备做一个游戏:两人分别掷一次骰子,谁掷出的骰子朝上的点数最大谁就获胜.现小明先掷,掷出的点数为4,请分别求出小明与小颖获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
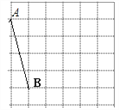
【题目】如图网格中每个小正方形的边长均为1,线段AB、CD的端点都在小正方形的顶点上.
(1)图(1)中,画一个以线段AB一边的四边形ABEF,且四边形ABEF是面积为7的中心对称图形,点E、F都在小正方形的顶点上,并直接写出线段BE的长;
(2)在图(2)中,画一个以线段CD为斜边直角三角形CDG,且△CDG的面积是2,点G在小方形的顶点上。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(﹣1,4)和点P(m,n)
(1)求这个一次函数的解析式;
(2)当n=2时,求直线AB,直线OP与x轴围成的图形的面积;
(3)当△OAP的面积等于△OAB的面积的2倍时,求n的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com