
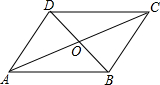
 如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )| A. | $\overrightarrow{OA}$ | B. | $\overrightarrow{OB}$ | C. | $\overrightarrow{OC}$ | D. | $\overrightarrow{OD}$ |
分析 由四边形ABCD是平行四边形根据平行四边形法则,可求得$\overrightarrow{BC}$=$\overrightarrow{AD}$=$\overrightarrow{n}$,然后由三角形法则,求得$\overrightarrow{AC}$与$\overrightarrow{BD}$,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴$\overrightarrow{BC}$=$\overrightarrow{AD}$=$\overrightarrow{n}$,
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{m}$+$\overrightarrow{n}$,$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$=$\overrightarrow{n}$-$\overrightarrow{m}$,
∴$\overrightarrow{OA}$=-$\frac{1}{2}$$\overrightarrow{AC}$=-$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$),$\overrightarrow{OC}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$),$\overrightarrow{OB}$=-$\frac{1}{2}$$\overrightarrow{BD}$=-$\frac{1}{2}$($\overrightarrow{n}$-$\overrightarrow{m}$),$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{n}$-$\overrightarrow{m}$).
故选C.
点评 此题考查了平面向量的知识以及平行四边形的性质.注意掌握三角形法则与平行四边形法则的应用是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm.
如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
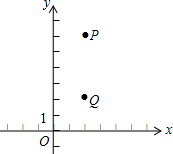 在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.
在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2$\sqrt{3}$cm,E为AB的中点,P为AD上一点,PE+PB的最小值为2$\sqrt{3}$.
如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2$\sqrt{3}$cm,E为AB的中点,P为AD上一点,PE+PB的最小值为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | c<b<a | D. | a<b<c |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
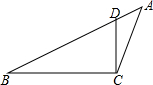 如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )
如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )| A. | ①、②、③ | B. | ①、③、④ | C. | ②、③、④ | D. | ①、②、④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com