
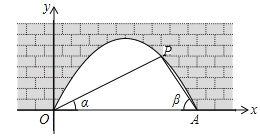
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
【答案】(1)P(3,![]() );(2)2.8米.
);(2)2.8米.
【解析】
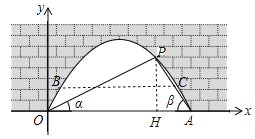
试题分析:(1)过点P作PH⊥OA于H,如图,设PH=3x,运用三角函数可得OH=6x,AH=2x,根据条件OA=4可求出x,即可得到点P的坐标;
(2)若水面上升1m后到达BC位置,如图,运用待定系数法可求出抛物线的解析式,然后求出y=1时x的值,就可解决问题.
试题解析:(1)过点P作PH⊥OA于H,如图.
设PH=3x,在Rt△OHP中,∵tanα=![]() ,∴OH=6x.
,∴OH=6x.
在Rt△AHP中,∵tanβ=![]() =
=![]() ,∴AH=2x,∴OA=OH+AH=8x=4,∴x=
,∴AH=2x,∴OA=OH+AH=8x=4,∴x=![]() ,∴OH=3,PH=
,∴OH=3,PH=![]() ,∴点P的坐标为(3,
,∴点P的坐标为(3,![]() );
);
(2)若水面上升1m后到达BC位置,如图,过点O(0,0),A(4,0)的抛物线的解析式可设为y=ax(x﹣4),∵P(3,![]() )在抛物线y=ax(x﹣4)上,∴3a(3﹣4)=
)在抛物线y=ax(x﹣4)上,∴3a(3﹣4)=![]() ,解得a=
,解得a=![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
当y=1时,![]() ,解得
,解得![]() ,
,![]() ,∴BC=(
,∴BC=(![]() )﹣(
)﹣(![]() )=
)=![]() =2×1.41=2.82≈2.8.
=2×1.41=2.82≈2.8.
答:水面上升1m,水面宽约为2.8米.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
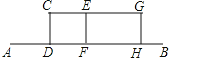
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新田为实现全县“脱贫摘帽”,2018年2月已统筹整合涉农资金235000000元,撬动800000000元金融资本参与全县脱贫攻坚工作,请将235000000用科学记数法表示为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是一个正方体骰子的表面展开图,将其折叠成正方体骰子,请根据要求回答问题: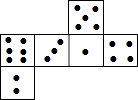
(1)如果1点在上面,3点在左面,几点在前面?
(2)如果3点在下面,几点在上面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需元,购买12根跳绳需元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com