
解:(1)由点A在抛物线上,得a=1,
由点B在抛物线上,
n=m
2=4,得:B(-2,4)
过Q点作x轴的平行线EF,过点A、B作x轴垂线分别交EF于F、E点,
设点Q (x
1,y
1),E (-2,y
1),F(1,y
1),
又可证得:△QFA∽△QEB,
∴

=

=

=2,EQ=2QF,EB=2AF,
EQ=x
1+2,QF=1-x
1,
∴x
1+2=2(1-x
1),x
1=0,
同理得:EB=4-y
1,AF=y
1-1,4-y
1=2 (y
1-1),y
1=2
∴Q(0,2);
(2)由题意知:Q,P,M三点在同一条垂直于x轴的直线上,
点P(x,y),则M (x,x
2),
设Q(x,y
1),
由QM=2MP得:y
1-x
2=2(x
2-y),y
1=3x
2-2y ①
由(1)知:EQ=2QF,EB=2AF,
EQ=x-m,QF=1-x,x-m=2(1-x) ②
EB=n-y
1,AF=y
1-1,n-y
1=2 (y
1-1)③
由②得:m=3x-2
由③得:n=3y
l-2=3(3x
2-2y)-2=9x
2-6y-2,
又∵点B在抛物线上
∴n=m
2,即:9x
2-6y-2=( 3x-2)
2解得:y=2x-1.
分析:(1)将点A(1,1)代入抛物线y=ax
2,可求抛物线的解析式,根据点B在抛物线上,则n=m
2=4,可得B(-2,4),过Q点作x轴的平行线EF,过点A、B作x轴垂线分别交EF于F、E点,设点Q (x
1,y
1),E (-2,y
1),F(1,y
1),根据相似三角形的判定和性质可得点Q的坐标;
(2)由题意知:Q,P,M三点在同一条垂直于x轴的直线上,点P(x,y),则M (x,x
2),设Q(x,y
1),由QM=2MP得:y
1-x
2=2(x
2-y),y
1=3x
2-2y ①由(1)知:EQ=2QF,EB=2AF,EQ=x-m,QF=1-x,x-m=2(1-x)②,EB=n-y
1,AF=y
1-1,n-y
1=2 (y
1-1)③,依此即可得到点P(x,y)的纵坐标y与横坐标x满足的解析式.
点评:考查了二次函数综合题,该题涉及到利用待定系数法确定函数解析式、相似三角形的判定和性质,方程组的求解等重点知识,同时注意辅助线的作法.

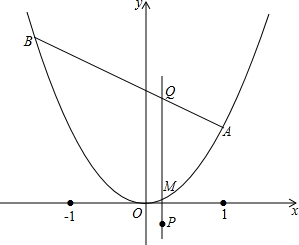 如图,抛物线y=ax2过点A(1,1),点B(m,n)在抛物线上运动,在线段AB上取一点Q,使得BQ=2QA.
如图,抛物线y=ax2过点A(1,1),点B(m,n)在抛物线上运动,在线段AB上取一点Q,使得BQ=2QA. 解:(1)由点A在抛物线上,得a=1,
解:(1)由点A在抛物线上,得a=1, =
= =
= =2,EQ=2QF,EB=2AF,
=2,EQ=2QF,EB=2AF,

 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).