
【题目】如图,根据图中数据完成填空,再按要求答题:

(1)sin2A1+sin2B1= . sin2A2+sin2B2= .sin2A3+sin2B3= ;
(2)观察上述等式,猜想在Rt△ABC中,∠C=90°,都有sin2A+sin2B= ;
(3)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、 ∠C 的对边分别是a、b、c,利用三角函数的定义和勾股定理,证明你的猜想;
(4)已知∠A+∠B =90°且sinA=![]() ,求sinB.
,求sinB.
【答案】(1)1 1 1;(2)1;(3)证明见解析;(4)![]() .
.
【解析】(1)由前面的结论,即可猜想出:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=1;
(2)在Rt△ABC中,∠C=90°.利用锐角三角函数的定义得出sinA=![]() ,sinB=
,sinB=![]() ,
,
则sin2A+sin2B=![]() ,再根据勾股定理得到a2+b2=c2,从而证明sin2A+sin2B=1;
,再根据勾股定理得到a2+b2=c2,从而证明sin2A+sin2B=1;
(3)利用关系式sin2A+sin2B=1,结合已知条件sinA=![]() ,进行求解.
,进行求解.
试题解析::(1)由图可知:sin2A1+sin2B1=(![]() )2+(
)2+(![]() )2=1;
)2=1;
sin2A2+sin2B2=(![]() )2+(
)2+(![]() )2=1;
)2=1;
sin2A3+sin2B3=(![]() )2+(
)2+(![]() )2=1.
)2=1.
观察上述等式,可猜想:sin2A+sin2B=1.
(2)如图,在Rt△ABC中,∠C=90°.
∵sinA=![]() ,sinB=
,sinB=![]() ,,
,,
∴sin2A+sin2B=![]() ,
,
∵∠C=90°,
∴a2+b2=c2,
∴sin2A+sin2B=1.
(3)∵sinA= ![]() ,sin2A+sin2B=1,
,sin2A+sin2B=1,
∴sinB=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. 4a3·2a2=8a6 B. (-2x4)·(-3x4)=6x8
C. 5x3·3x4=8x7 D. (-x)·(-2x)2·(-3x)3=-108x6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=2![]() .点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.
.点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.
(1)求这条抛物线的解析式;
(2)用含m的代数式表示线段CO的长;
(3)当tan∠ODC=![]() 时,求∠PAD的正弦值.
时,求∠PAD的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
![]()
![]()
![]()
……
计算:3×(1×2+2×3+3×4+…+99×100)= ( )
A. 97×98×99 B. 98×99×100 C. 99×100×101 D. 100×101×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形![]() 的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①.
的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①.
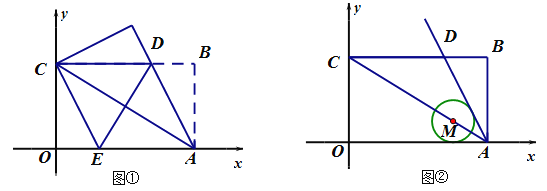
(1)求点![]() 的坐标和
的坐标和![]() 所在直线的函数关系式;
所在直线的函数关系式;
(2)![]() 的圆心
的圆心![]() 始终在直线
始终在直线![]() 上(点
上(点![]() 除外),且
除外),且![]() 始终与x轴相切,如图②.
始终与x轴相切,如图②.
①求证: ![]() 与直线AD相切;
与直线AD相切;
②圆心![]() 在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时
在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时![]() 与x轴、y轴和直线AD都相切时的圆心
与x轴、y轴和直线AD都相切时的圆心![]() 的坐标;如果不能相切,请说明理由.
的坐标;如果不能相切,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com