
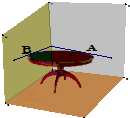
 小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )| A、45° |
| B、135° |
| C、45°或135° |
| D、90°或135° |
科目:初中数学 来源: 题型:
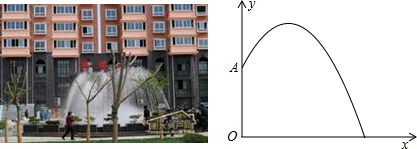
 在“母亲节”期间,某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价(整数)x(元/个)之间的对应关系如图所示:
在“母亲节”期间,某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价(整数)x(元/个)之间的对应关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
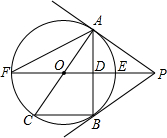 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D.交⊙O于点A,延长AD与⊙0交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D.交⊙O于点A,延长AD与⊙0交于点C,连接BC,AF.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 年龄 | 20 | 22 | 23 | 25 | 28 | 30 | 32 |
| 人数 | 1 | 2 | 1 | 3 | 2 | 1 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某学校为了了解该学校七年级学生双休日上网的情况,随机调查了该学校七年级的25名学生,得到了上周双休日上网时间的一组样本数据,其频数分布直方图如图所示,那么估计该学校七年级每名学生双休日上网的平均时间是( )
某学校为了了解该学校七年级学生双休日上网的情况,随机调查了该学校七年级的25名学生,得到了上周双休日上网时间的一组样本数据,其频数分布直方图如图所示,那么估计该学校七年级每名学生双休日上网的平均时间是( )| A、3.2小时 |
| B、3.4小时 |
| C、3.5小时 |
| D、3.6小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com