
阅读某同学解下面分式方程的过程
解方程![]() +
+![]() =
=![]() +
+![]()
解:![]() -
-![]() =
=![]() -
-![]() ①
①
![]() =
=![]() ②
②
![]() =
=![]() ③
③
∴x2-6x+8=x2-4x+3
∴x=![]() 经检验,x=
经检验,x=![]() 是原方程的解.
是原方程的解.
请你回答:
(1)得到①式的做法是________;
得到②式的做法是________;
得到③式的理由是________.
(2)上述解答对吗?若不对,找出错误,并加以改正.
科目:初中数学 来源: 题型:
| 1 |
| x-4 |
| 4 |
| x-1 |
| 2 |
| x-3 |
| 3 |
| x-2 |
| 1 |
| x-4 |
| 3 |
| x-2 |
| 2 |
| x-3 |
| 4 |
| x-1 |
| -2x+10 |
| x2-6x+8 |
| -2x+10 |
| x2-4x+3 |
| 1 |
| x2-6x+8 |
| 1 |
| x2-4x+3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| x-4 |
| 4 |
| x-1 |
| 2 |
| x-3 |
| 3 |
| x-2 |
| 1 |
| x-4 |
| 3 |
| x-2 |
| 2 |
| x-3 |
| 4 |
| x-1 |
| -2x+10 |
| x2-6x+8 |
| -2x+10 |
| x2-4x+3 |
| 1 |
| x2-6x+8 |
| 1 |
| x2-4x+3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
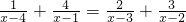 .
.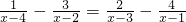 ,①
,①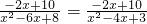 ,②
,②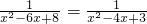 ,③
,③ .
. 代入原方程检验知
代入原方程检验知 是原方程的解.
是原方程的解.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| x-4 |
| 4 |
| x-1 |
| 2 |
| x-3 |
| 3 |
| x-2 |
| 1 |
| x-4 |
| 3 |
| x-2 |
| 2 |
| x-3 |
| 4 |
| x-1 |
| -2x+10 |
| x2-6x+8 |
| -2x+10 |
| x2-4x+3 |
| 1 |
| x2-6x+8 |
| 1 |
| x2-4x+3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:月考题 题型:解答题
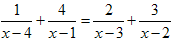
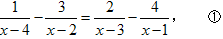
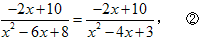
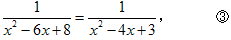

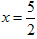 ,
, 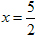 代入原方程检验知
代入原方程检验知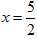 是原方程的解,请你回答:
是原方程的解,请你回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com