
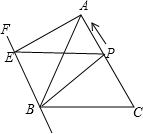
 如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.
如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.分析 (1)利用已知结合AP=AC-PC,进而得出答案;
(2)利用平行四边形的性质得出AP=BE,进而求出即可;
(3)利用梯形的面积求法得出四边形BPAE的面积=$\frac{1}{2}$(AP+BE)×BG进而求出即可.
解答 解:(1)由题意可得:CP=2t,AC=13cm,则AP=13-2t;
(2)当BE=AP时,四边形BPAE是平行四边形,
∵PE∥BC,BF∥AC,
∴四边形EBCP是平行四边形,
∴EB=PC,
即 2t=13-2t,
解得:t=$\frac{13}{4}$,
故t=$\frac{13}{4}$秒时,四边形BPAE为平行四边形;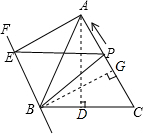
(3)过点A作AD⊥BC于点D,过点B作BP⊥AC于点G,
∵AB=AC=13cm,BC=10cm,
∴AD=12cm,则AD×BC=AC×BG,即12×10=13×BG,
解得:BG=$\frac{120}{13}$,
∵BE=2t,AP=13-2t,
∴AP+BE=13,
∴四边形BPAE的面积=$\frac{1}{2}$(AP+BE)×BG=$\frac{13}{2}$×$\frac{120}{13}$=60(cm2).
点评 此题主要考查了平行四边形的性质以及梯形面积求法和等腰三角形的性质,得出BG的长是解题关键.


科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,点A是抛物线y=a(x-4)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为24.
在平面直角坐标系中,点A是抛物线y=a(x-4)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.62×104m2 | B. | 56.2×104m2 | C. | 5.62×105m2 | D. | 0.562×104m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(环) | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 3 | 2 | 3 | 1 |
| A. | 极差是2环 | B. | 中位数是8环 | C. | 众数是9环 | D. | 平均数是9环 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com