
| 成绩(环) | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 3 | 2 | 3 | 1 |
| A. | 极差是2环 | B. | 中位数是8环 | C. | 众数是9环 | D. | 平均数是9环 |
分析 根据极差反映了一组数据变化范围的大小,求极差的方法是用一组数据中的最大值减去最小值,以及众数是出现次数最多的数,中位数是按大小顺序排列后,最中间的一个即是中位数,所有数据的和除以数据个数即是平均数,分别求出即可.
解答 解:A、极差是10-6=4环,故本选项错误;
B、把数从小到大排列起来;6,7,7,7,8,8,9,9,9,10,位于中间的两个数都是8,所以中位数是(8+8)÷2=8,故本选项正确;
C、7和9都出现了3次,次数最多,所以众数是7环和9环,故本选项错误;
D、平均数=$\frac{1}{10}$(6+7×3+8×2+9×3+10)=8,故本选项错误;
故选:B.
点评 此题主要考查了极差,平均数,众数与中位数,解决问题的关键是正确把握这几种数概念的区别与联系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
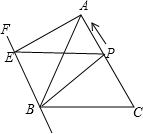 如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.
如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
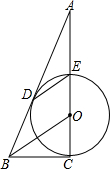 如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.
如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
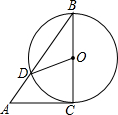 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠BAC=55°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠BAC=55°,则∠COD的大小为( )| A. | 70° | B. | 60° | C. | 55° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
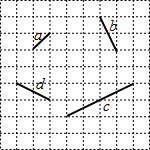 如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )| A. | 3种 | B. | 6种 | C. | 8种 | D. | 12种 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
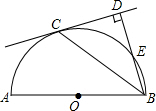 如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com