
分析 (1)设制作每个乙盒用x米材料,则制作甲盒用(1+20%)x米材料,根据“同样用6m材料制成甲盒的个数比制成乙盒的个数少2个”,列出方程,即可解答;
(2)根据所需要材料的总长度l=甲盒材料的总长度+乙盒材料的总长度,列出函数关系式;再根据“甲盒的数量不少于乙盒数量的2倍”求出n的取值范围,根据一次函数的性质,即可解答.
解答 解:(1)设制作每个乙盒用x米材料,则制作甲盒用(1+20%)x米材料,
$\frac{6}{x}-2=\frac{6}{(1+20%)x}$,
解得:x=0.5,
经检验x=0.5是原方程的解,
∴(1+20%)x=0.6(米),
答:制作每个甲盒用0.6米材料;制作每个乙盒用0.5米材料.
(2)根据题意得:l=0.6n+0.5(3000-n)=0.1n+1500,
∵甲盒的数量不少于乙盒数量的2倍,
∴n≥2(3000-n)
解得:n≥2000,
∴2000≤n<3000,
∵k=0.1>0,
∴l随n增大而增大,
∴当n=2000时,l最小1700米.
点评 本题考查了一次函数的应用,解决本题的关键是利用一次函数的性质解决实际问题.


科目:初中数学 来源: 题型:选择题
| A. | 0.6×1013元 | B. | 60×1011元 | C. | 6×1012元 | D. | 6×1013元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(环) | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 3 | 2 | 3 | 1 |
| A. | 极差是2环 | B. | 中位数是8环 | C. | 众数是9环 | D. | 平均数是9环 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
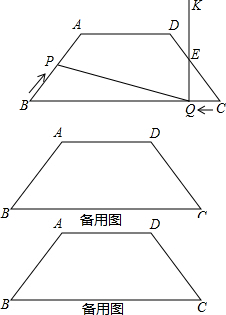 如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12,点P从点B出发沿折线段BA-AD-DC以每秒1个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒$\frac{3}{5}$个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E;点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止,设P、Q运动的时间为t秒(t>0).
如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12,点P从点B出发沿折线段BA-AD-DC以每秒1个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒$\frac{3}{5}$个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E;点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止,设P、Q运动的时间为t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
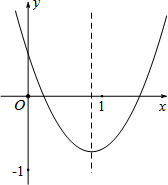 已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 4个以上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com