练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，已知l1∥l2∥l3，AC，DF交于点O，且
    AB
    BC
    =
    n
    m
    ，求证：
    DE
    DF
    =
    n
    m+n
    ．
    考点：平行线分线段成比例
    专题：证明题
    分析：根据平行线分线段成比例定理得
    DE
    DF
    =
    AB
    AC
    ，再利用比例性质由
    AB
    BC
    =
    n
    m
    得到
    AB
    AC
    =
    n
    m+n
    ，所以
    DE
    DF
    =
    n
    m+n
    ．
    解答：证明：∵l1∥l2∥l3，
    ∴
    DE
    DF
    =
    AB
    AC
    ，
    ∵
    AB
    BC
    =
    n
    m
    ，
    ∴
    AB
    AB+BC
    =
    n
    n+m
    ，即
    AB
    AC
    =
    n
    m+n
    ，
    ∴
    DE
    DF
    =
    n
    m+n
    ．
    点评：本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    下列方程中，以x=
    1
    2
    为解的是（　　）
    A、2x-4=0
    B、2x-1=x+1
    C、3-4x=2x-3
    D、2x-1=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    设地面气温为20℃，如果每升高1km，气温下降6℃．如果高度用h（km）表示，气温用t（℃）表示，那么t随h的变化而变化的关系式为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

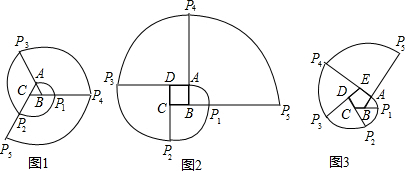
    （1）如图1，边长为1的正三角形ABC，曲线AP1P2P3P4P5…叫做“正三角形的渐开线”，其中，AP1、P1P2、P2P3、P3P4、P4P5…的圆心依次按B、C、A、B、C…循环，由题意可求得：曲线AP1P2P3P4P5的长度为
     
    ；如果按这样的规律一直持续下去，则曲线AP1P2P3P4P5…Pn的长度为
     
    ．
    （2）如图2，边长为1的正四边形ABCD，曲线AP1P2P3P4P5…叫做“正四边形的渐开线”，其中，AP1、P1P2、P2P3、P3P4、P4P5…的圆心依次按B、C、D、A、B…循环，由题意可求得：曲线AP1P2P3P4P5的长度为
     
    ；如果按这样的规律一直持续下去，则曲线AP1P2P3P4P5…Pn的长度为
     
    ．
    （3）如图3，边长为1的正五边形ABCDE，曲线AP1P2P3P4P5…叫做“正五边形的渐开线”，其中，AP1、P1P2、P2P3、P3P4、P4P5…的圆心依次按B、C、D、E、A…循环，由题意可求得：曲线AP1P2P3P4P5的长度为
     
    ；如果按这样的规律一直持续下去，则曲线AP1P2P3P4P5…Pn的长度为
     
    ．
    （4）由以上结论猜想：边长为1的正m边形，曲线AP1P2P3P4P5…叫做“正m边形的渐开线”，其中，AP1、P1P2、P2P3、P3P4、P4P5…的圆心依次按B、C、D、E、F…循环，则曲线AP1P2P3P4P5…Pn的长度为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

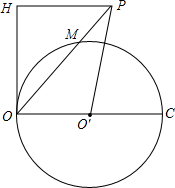    如图，点P为圆O′外一点，OC为圆O′的直径，PO=OC，PO交圆O′于M，OH为圆O′的切线，且PH垂直于OH，若OH=2PM，求tan∠OPO′的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在⊙O中，
    AB
    =
    AC
    ，∠ACB=60°．
    （1）求证：∠AOB=∠BOC=∠AOC；
    （2）若D是
    AB
    的中点，求证：四边形OADB是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一个直角三角形的两条直角边的长分别为2
    		2
    cm与
    		10
    cm，求这个直角三角形的面积和周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    表示实数x的点到原点的距离为2
    		3
    ，则数x为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    把二次函数y=x2-2x+3配方成y=a（x-k）2+h的形式，并求出它的图象的顶点坐标、对称轴方程，y＜0时x的取值范围，并画出图象．

    查看答案和解析>>

    同步练习册答案