
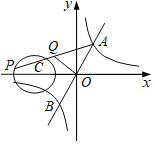
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
如图,连接BP,由反比例函数的对称性质以及三角形中位线定理可得OQ=![]() BP,再根据OQ的最大值从而可确定出BP长的最大值,由题意可知当BP过圆心C时,BP最长,过B作BD⊥x轴于D,继而根据正比例函数的性质以及勾股定理可求得点B坐标,再根据点B在反比例函数y=
BP,再根据OQ的最大值从而可确定出BP长的最大值,由题意可知当BP过圆心C时,BP最长,过B作BD⊥x轴于D,继而根据正比例函数的性质以及勾股定理可求得点B坐标,再根据点B在反比例函数y=![]() (k>0)的图象上,利用待定系数法即可求出k的值.
(k>0)的图象上,利用待定系数法即可求出k的值.
如图,连接BP,
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=![]() BP,
BP,
∵OQ长的最大值为![]() ,
,
∴BP长的最大值为![]() ×2=3,
×2=3,
如图,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t﹣(﹣2)=t+2,BD=﹣2t,
在Rt△BCD中,由勾股定理得: BC2=CD2+BD2,
∴22=(t+2)2+(﹣2t)2,
t=0(舍)或t=﹣![]() ,
,
∴B(﹣![]() ,﹣
,﹣![]() ),
),
∵点B在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴k=﹣![]() ×(-
×(-![]() )=
)=![]() ,
,
故选C.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】某工厂将地处A,B两地的两个小工厂合成一个大厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修一条笔直的公路(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一以C点为中心,半径为0.7km的圆形公园,则修筑的这条公路会不会穿过公园?为什么?(提示:判断以点C为圆心的圆与AB的关系)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
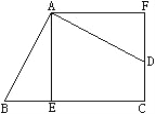
【题目】如图,四边形ABCD的∠BAD=∠C=90,AB=AD,AE⊥BC于E,![]() 旋转后能与
旋转后能与![]() 重合.
重合.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5㎝,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
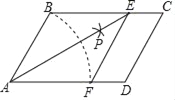
【题目】如图,在ABCD中,以点4为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的长为半径画弧,两弧交于点P;连接AP并廷长交BC于点E,连接EF
BF的长为半径画弧,两弧交于点P;连接AP并廷长交BC于点E,连接EF
(1)根据以上尺规作图的过程,求证:四边形ABEF是菱形;
(2)若AB=2,AE=2![]() ,求∠BAD的大小.
,求∠BAD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是 事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每8个人中会有1人抽中一等奖,2人抽中二等奖,若袋中共有24个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中减少3个白球,那么抽奖一次恰好抽中一等奖的概率是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知a=3,b和c是关于x的方程x2+mx+2-![]() m=0的两个实数根.
m=0的两个实数根.
(1)求△ABC的周长.
(2)求△ABC的三边均为整数时的外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,直角边为a、b,斜边为c.若把关于x的方程ax2+![]() cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 一定有实数根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com