
【题目】在等腰三角形ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知a=3,b和c是关于x的方程x2+mx+2-![]() m=0的两个实数根.
m=0的两个实数根.
(1)求△ABC的周长.
(2)求△ABC的三边均为整数时的外接圆半径.
【答案】(1)△ABC的周长为7![]() 或7;(2)△ABC的三边均为整数时的外接圆半径为
或7;(2)△ABC的三边均为整数时的外接圆半径为![]() .
.
【解析】
(1)此题分两种情况考虑:一是b和c中有一个和a相等,是3;二是b=c,即根据方程有两个相等的实数根,由△=0求解.最后注意看是否符合三角形的三边关系.
(2)根据(1)中求解的结果,只需求得2,3,3的三角形的外接圆的半径,根据等腰三角形的三线合一和勾股定理求解.
(1)若b、c中有一边等于3,
则方程可化为![]() ,
,
解得m=-![]() ;
;
原方程可化为x2-![]() =0,
=0,
解得x1=3,x2=![]() ,
,
所以三角形的周长为3+3+![]() =
=![]() ;
;
若b=c,则△=m2-4(![]() )=0,
)=0,
解得m=﹣4或2,
当m=﹣4时,方程为x2﹣4x+4=0,得x1=x2=2,
所以三角形的周长为2+2+3=7;
当m=2时,方程为x2+2x+1=0,得x1=x2=﹣1;(不合题意,舍去)
综上可知△ABC的周长为7![]() 或7.
或7.
(2)作△ABC的外接圆⊙O,连接AO并延长交⊙O于点D、交BC于E,连接BO,
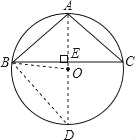
则有AE⊥BC.
∵△ABC的三边均为整数,
∴AB=AC=2,BC=3,
BE=![]() BC=
BC=![]() .AE=
.AE=![]() =
=![]() ,
,
设AO=R,在Rt△BOE中,R2=(![]() )2+(
)2+(![]() ﹣R)2,
﹣R)2,
∴R=![]() ,
,
∴△ABC的三边均为整数时的外接圆半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线l![]() 在平面直角坐标系中,直线l
在平面直角坐标系中,直线l![]() 与y轴交于点A,点B(-3,3)也在直线1上,将点B先向右平移1个单位长度、再向下平移2个单位长度得到点C,点C恰好也在直线l
与y轴交于点A,点B(-3,3)也在直线1上,将点B先向右平移1个单位长度、再向下平移2个单位长度得到点C,点C恰好也在直线l![]() 上。
上。
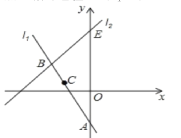
(1)求点C的坐标和直线l![]() 的解析式
的解析式
(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l![]() 上;
上;
(3)已知直线l![]() :y=x+b经过点B,与y轴交于点E,求△ABE的面积。
:y=x+b经过点B,与y轴交于点E,求△ABE的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
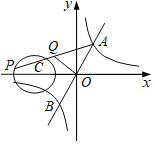
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中小正方形的边长为1,![]() (0,4).
(0,4).
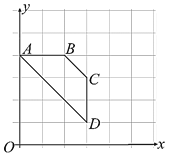
(1) 在图中标出点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() ,
,![]() ,
,![]() 的距离都相等;
的距离都相等;
(2) 连接![]() ,
,![]() ,
,![]() ,此时
,此时![]() 是___________三角形;
是___________三角形;
(3) 四边形![]() 的面积是___________.
的面积是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
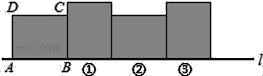
【题目】如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A在整个旋转过程中所经过的路程之和是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)设商场每件商品降价x元,利润为y元,写出y与x的函数关系式。
(2)当该商品的销售价为多少元时,所获利润最大?最大利润是多少?
(3)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com