
【题目】如图,在平面直角坐标系中,抛物线y=x2+2x-3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l,点D(-4,n)在抛物线上.
(1)求直线CD的解析式;
(2)E为直线CD下方抛物线上的一点,连接EC,ED,当△ECD的面积最大时,在直线l上取一点M,过M作y轴的垂线,垂足为点N,连接EM,BN,若EM=BN时,求EM+MN+BN的值.
(3)将抛物线y=x2+2x-3沿x轴正方向平移得到新抛物线y′,y′经过原点O,y′与x轴的另一个交点为F,设P是抛物线y′上任意一点,点Q在直线l上,△PFQ能否成为以点P为直角顶点的等腰直角三角形?若能,直接写出点P的坐标,若不能,请说明理由.

【答案】(1)直线CD的解析式为y=-2x-3;(2)1+![]() ;(3)存在.满足条件的点P坐标为(
;(3)存在.满足条件的点P坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)求出C、D两点坐标,利用待定系数法即可解决问题;
(2)如图1中,过点E作EG∥y轴交直线CD于G.设E(m,m2+2m﹣3).则G(m,﹣2m﹣3),GE=﹣m2﹣4m.根据S△EDC=![]() EG|Dx|=
EG|Dx|=![]() (﹣m2﹣4m)×4=﹣2(m+2)2+8,可知m=﹣2时,△DEC的面积最大,此时E(﹣2,﹣3),再证明Rt△EHM≌Rt△BON即可解决问题;
(﹣m2﹣4m)×4=﹣2(m+2)2+8,可知m=﹣2时,△DEC的面积最大,此时E(﹣2,﹣3),再证明Rt△EHM≌Rt△BON即可解决问题;
(3)存在.如图2中.作P1M⊥x轴于M,P1N⊥对称轴l于N.对称轴l交OA于K,由△P1MF≌△P1NQ,推出P1M=P1N,推出点P在∠MKN的角平分线上,只要求出直线KP1的解析式,构建方程组即可解决问题,同法可求P3,P4.
(1)由题意得:C(0,﹣3),D(﹣4,5),设直线CD的解析式为y=kx+b,则有![]() ,解得:
,解得:![]() ,∴直线CD的解析式为y=﹣2x﹣3.
,∴直线CD的解析式为y=﹣2x﹣3.
(2)如图1中,过点E作EG∥y轴交直线CD于G.设E(m,m2+2m﹣3).则G(m,﹣2m﹣3),GE=﹣m2﹣4m.

∴S△EDC=![]() EG|Dx|=
EG|Dx|=![]() (﹣m2﹣4m)×4=﹣2(m+2)2+8.
(﹣m2﹣4m)×4=﹣2(m+2)2+8.
∵﹣2<0,∴m=﹣2时,△DEC的面积最大,此时E(﹣2,﹣3).
∵C(0,﹣3),∴EC∥AB,设CE交对称轴于H.
∵B(1,0),∴EH=OB=1.
∵EM=BN,∴Rt△EHM≌Rt△BON,∴MH=ON=![]() OC=
OC=![]() ,∴EM=BN=
,∴EM=BN=![]() =
=![]() ,∴EM+MN+BN=1+
,∴EM+MN+BN=1+![]() .
.
(3)存在.如图2中.作P1M⊥x轴于M,P1N⊥对称轴l于N.对称轴l交OA于K.

由P1Q=P1F,∠QP1F=90°,可得△P1MF≌△P1NQ,∴P1M=P1N,∴点P在∠MKN的角平分线上.
∵直线KP1的解析式为y=﹣x﹣1,抛物线y′的解析式为y=x2﹣4x,由![]() ,解得:
,解得: 或
或 ,∴P1(
,∴P1(![]() ),P2(
),P2(![]() ),同法可知,直线y=x+1与抛物线的交点P3,P4也符合条件.
),同法可知,直线y=x+1与抛物线的交点P3,P4也符合条件.
由![]() ,解得:
,解得: 或
或 ,∴P3(
,∴P3(![]() ),P4(
),P4(![]() ).
).
综上所述:满足条件的点P坐标为(![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△ABE∽△ACD,③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
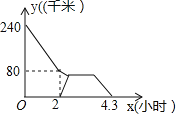
【题目】老张匀速开车从A市送货到B市,途中汽车出现小故障,老张只能降速为原速的一半行驶等待B市的修车师傅小李前往修车,半小时后,小李与老张相遇,立马开始修车,车修好后,老张又提速为原速的![]() 继续开车送货到B市,小李以原速返回B市,老张和小李距离B市的路程y(千米)与老张出发的时间x(小时)的函数图象分别如图所示(途中其它损耗时间忽略不计),则小李在返回到B市时,老张距B市______千米.
继续开车送货到B市,小李以原速返回B市,老张和小李距离B市的路程y(千米)与老张出发的时间x(小时)的函数图象分别如图所示(途中其它损耗时间忽略不计),则小李在返回到B市时,老张距B市______千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
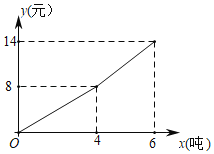
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上收费标准(收费标准:每吨水的价格)某用户每月应交水费y(元)与用水量x(吨)之间关系的图象如图:
(1)说出自来水公司在这两个用水范围内的收费标准;
(2)当x>4时,求因变量y与自变量x之间的关系式;
(3)若某用户该月交水费26元,求他用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,BC=10,AC⊥AB,点E、F分别是BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形时,请求出AE的长度;
(3)若四边形AECF是矩形时,请直接写出BE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π);
(4)求出(2)△A2BC2的面积是多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
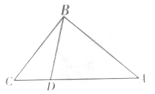
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上的动点,点
边上的动点,点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 运动,当运动到点
运动,当运动到点![]() 时停止,若设点
时停止,若设点![]() 运动的时间为
运动的时间为![]() 秒,点
秒,点![]() 运动的速度为每秒2个单位长度.
运动的速度为每秒2个单位长度.

(1)当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
(2)求当![]() 为何值时,
为何值时,![]() 是直角三角形,说明理由;
是直角三角形,说明理由;
(3)求当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画。要求每位同学必须参加,且限报一项活动。以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图。请你结合图示所给出的信息解答下列问题。

(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com