
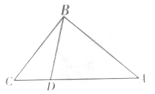
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上的动点,点
边上的动点,点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 运动,当运动到点
运动,当运动到点![]() 时停止,若设点
时停止,若设点![]() 运动的时间为
运动的时间为![]() 秒,点
秒,点![]() 运动的速度为每秒2个单位长度.
运动的速度为每秒2个单位长度.

(1)当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
(2)求当![]() 为何值时,
为何值时,![]() 是直角三角形,说明理由;
是直角三角形,说明理由;
(3)求当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
【答案】(1)CD=4,AD=16;(2)当t=3.6或10秒时,![]() 是直角三角形,理由见解析;(3)当t=7.2秒时,
是直角三角形,理由见解析;(3)当t=7.2秒时,![]() ,理由见解析
,理由见解析
【解析】
(1)根据CD=速度×时间列式计算即可得解,利用勾股定理列式求出AC,再根据AD=AC-CD代入数据进行计算即可得解;
(2)分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解;
(3)过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答.
解:(1)t=2时,CD=2×2=4,
∵∠ABC=90°,AB=16,BC=12,
![]()
∴AD=AC-CD=20-4=16;
(2)①∠CDB=90°时,![]()
∴![]() 解得BD=9.6,
解得BD=9.6,
∴![]()
t=7.2÷2=3.6秒;
②∠CBD=90°时,点D和点A重合,
t=20÷2=10秒,
综上所述,当t=3.6或10秒时,![]() 是直角三角形;
是直角三角形;
(3)如图,过点B作BF⊥AC于F,
由(2)①得:CF=7.2,
∵BD=BC,
∴CD=2CF=7.2×2=14.4,
∴t=14.4÷2=7.2,
∴当t=7.2秒时,![]() ,
,


科目:初中数学 来源: 题型:
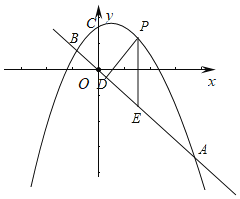
【题目】如图,已知抛物线y=-x2+bx+c与直线y=-x的交点A、B的横坐标分别为2和![]() .点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
.点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
(1)直接写出点A、B的坐标;
(2)求抛物线的关系式;
(3)判断△OBC形状,并说明理由;
(4)设点P的横坐标为n,线段PD的长为y,求y关于n的函数关系式;
(5)定义符号min{a,b)}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如min{2,0}=0,min{-3,4}=-3.直接写出min{-x2+bx+c,-x}的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+2x-3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l,点D(-4,n)在抛物线上.
(1)求直线CD的解析式;
(2)E为直线CD下方抛物线上的一点,连接EC,ED,当△ECD的面积最大时,在直线l上取一点M,过M作y轴的垂线,垂足为点N,连接EM,BN,若EM=BN时,求EM+MN+BN的值.
(3)将抛物线y=x2+2x-3沿x轴正方向平移得到新抛物线y′,y′经过原点O,y′与x轴的另一个交点为F,设P是抛物线y′上任意一点,点Q在直线l上,△PFQ能否成为以点P为直角顶点的等腰直角三角形?若能,直接写出点P的坐标,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
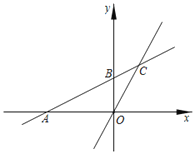
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=![]() x的图象交于点C(m,3).
x的图象交于点C(m,3).
(1)求一次函数y=kx+b(k≠0)的函数关系式;
(2)△AOC的面积为______;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,过点
,过点![]() 做直线
做直线![]() 平行于
平行于![]() 轴,点
轴,点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)点![]() 在直线
在直线![]() 上,且位于
上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在直线
恰好落在直线![]() 上,求点
上,求点![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(3)设点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求点
为等边三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中踏集团销售某种商品,每件进价为10元。在销售过程中发现,平均每天的销售量y(件)与销售价x(元/件)(不低于进价)之间的关系可近似的看做一次函数:![]() ;
;
(1)求中踏集团平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(2)当这种商品的销售价为多少元时,可以获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
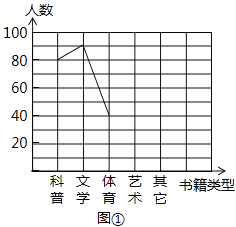
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
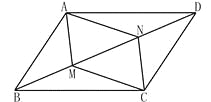
【题目】如图,M、N是平行四边形ABCD对角线BD上两点.
(1)若BM=MN=DN,求证:四边形AMCN为平行四边形;
(2)若M、N为对角线BD上的动点(均可与端点重合),设BD=12cm,点M由点B向点D匀速运动,速度为2(cm/s),同时点N由点D向点B匀速运动,速度为 a(cm/s),运动时间为t(s).若要使四边形AMCN为平行四边形,求a的值及t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com