
【题目】如图,M、N是平行四边形ABCD对角线BD上两点.
(1)若BM=MN=DN,求证:四边形AMCN为平行四边形;
(2)若M、N为对角线BD上的动点(均可与端点重合),设BD=12cm,点M由点B向点D匀速运动,速度为2(cm/s),同时点N由点D向点B匀速运动,速度为 a(cm/s),运动时间为t(s).若要使四边形AMCN为平行四边形,求a的值及t的取值范围.
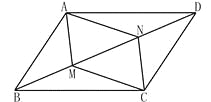
【答案】(1)证明见解析;(2)a=2,0≤t≤6且t≠3.
【解析】
试题(1)根据题意易证△AND≌△CMB.所以AN=CM,∠AND=∠CMB.所以∠ANM=∠CMN,即AN∥CM.因此,四边形AMCN为平行四边形;
(2)连接AC,交BD于O,要使四边形AMCN为平行四边形,即OM=ON,列出方程与不等式即可求解.
试题解析:(1)∵四边形ABCD是平行四边形
∴AD=CB,AD∥BC
∴∠ADB=∠CBD
又∵BM=DN
∴△AND≌△CBM
∴CM=AN,∠BMC=∠DNA
∴∠CMN=∠ANM
∴CM∥AN
∴四边形AMCN为平行四边形;
(2)如图,连接AC,交BD于O,要使四边形AMCN为平行四边形,即OM=ON,
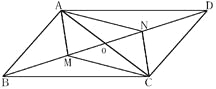
∴6-2t=6-at
∴a=2
当M、M重合于点O,即t=3时,点A、M、C、N在同一直线上,不能组成四边形,
∴0≤t≤6且t≠3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上的动点,点
边上的动点,点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 运动,当运动到点
运动,当运动到点![]() 时停止,若设点
时停止,若设点![]() 运动的时间为
运动的时间为![]() 秒,点
秒,点![]() 运动的速度为每秒2个单位长度.
运动的速度为每秒2个单位长度.
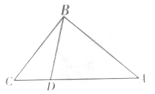

(1)当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
(2)求当![]() 为何值时,
为何值时,![]() 是直角三角形,说明理由;
是直角三角形,说明理由;
(3)求当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画。要求每位同学必须参加,且限报一项活动。以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图。请你结合图示所给出的信息解答下列问题。

(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
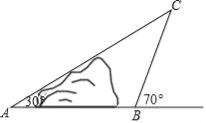
【题目】如图,地面上小山的两侧有![]() ,
,![]() 两地,为了测量
两地,为了测量![]() ,
,![]() 两地的距离,让一热气球从小山西侧
两地的距离,让一热气球从小山西侧![]() 地出发沿与
地出发沿与![]() 成
成![]() 角的方向,以每分钟
角的方向,以每分钟![]() 的速度直线飞行,
的速度直线飞行,![]() 分钟后到达
分钟后到达![]() 处,此时热气球上的人测得
处,此时热气球上的人测得![]() 与
与![]() 成
成![]() 角,请你用测得的数据求
角,请你用测得的数据求![]() ,
,![]() 两地的距离
两地的距离![]() 长.(结果用含非特殊角的三角函数和根式表示即可)
长.(结果用含非特殊角的三角函数和根式表示即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
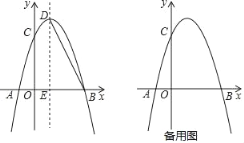
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBFG,随着点P的运动,正方形的大小、位置也随着改变,当顶点F或G恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组的同学在一次数学活动中,为了测量某建筑物AB的高,他们来到与建筑物AB在同一平地且相距12米的建筑物CD上的C处观察,测得某建筑物顶部A的仰角为30°、底部B的俯角为45°.求建筑物AB的高(精确到1米).(可供选用的数据:![]() ≈1.4,
≈1.4,![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com