
【题目】如图,射线![]() 上有三点
上有三点![]() 、
、![]() 、
、![]() ,满足
,满足![]() ,
, ![]() ,
, ![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 秒的速度匀速运动,点
秒的速度匀速运动,点![]() 从点
从点![]() 出发在线段
出发在线段![]() 上向点
上向点![]() 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 、
、![]() 停止运动.
停止运动.
(1)若点![]() 运动速度为
运动速度为![]() 秒,经过多长时间
秒,经过多长时间![]() 、
、![]() 两点相遇?
两点相遇?
(2)当![]() 在线段
在线段![]() 上且
上且![]() 时,点
时,点![]() 运动到的位置恰好是线段
运动到的位置恰好是线段![]() 的三等分点,
的三等分点,
求点![]() 的运动速度;
的运动速度;
(3)当点![]() 运动到线段
运动到线段![]() 上时,分别取
上时,分别取![]() 和
和![]() 的中点
的中点![]() 、
、![]() ,求
,求![]() 的值.
的值.
![]()
【答案】(1)30秒;(2)![]() 或
或![]() ;(3)2.
;(3)2.
【解析】试题分析:(1)从题中我们可以看出点P及Q是运动的,不是静止的,当PA=2PB时实际上是P正好到了AB的三等分点上,而且PA=40,PB=20.由速度公式就可求出它的运动时间,即是点Q的运动时间,点Q运动到的位置恰好是线段AB的三等分点,这里的三等分点是二个点,因此此题就有二种情况,分别是AQ=![]() 时,BQ=
时,BQ=![]() 时,由此就可求出它的速度.
时,由此就可求出它的速度.
(2)若点Q运动速度为3cm/s,经过多长时间P,Q两点相距70cm,这也有两种情况即当它们相向而行时,和它们直背而行时,此题可设运动时间为t秒,按速度公式就可解了.
(3)此题就可把它当成一个静止的线段问题来解决了,但必须借助图形.
试题解析:(1)①当P在线段AB上时,由PA=2PB及AB=60,可求得PA=40,OP=60,故点P运动时间为60秒.
若AQ=![]() 时,BQ=40,CQ=50,点Q的运动速度为50÷60=
时,BQ=40,CQ=50,点Q的运动速度为50÷60=![]() (cm/s),
(cm/s),
若BQ=![]() 时,BQ=20,CQ=30,点Q的运动速度为30÷60=
时,BQ=20,CQ=30,点Q的运动速度为30÷60=![]() (cm/s).
(cm/s).
②点P在线段AB延长线上时,由PA=2PB及AB=60,可求得PA=120,OP=140,故点P运动时间为140秒.
若AQ=![]() 时,BQ=40,CQ=50,点Q的运动速度为50÷140=
时,BQ=40,CQ=50,点Q的运动速度为50÷140=![]() (cm/s)
(cm/s)
若BQ=![]() 时,BQ=20,CQ=30,点Q的运动速度为30÷140=
时,BQ=20,CQ=30,点Q的运动速度为30÷140=![]() (cm/s).
(cm/s).
(2)设运动时间为t秒,则t+3t=90±70,t=5或40,
∵点Q运动到O点时停止运动,
∴点Q最多运动30秒,当点Q运动30秒到点O时PQ=OP=30cm,之后点P继续运动40秒,则PQ=OP=70cm,此时t=70秒,故经过5秒或70秒两点相距70cm,
(3)如图1,设OP=xcm,点P在线段AB上,20≤x≤80, OB-AP=80-(x-20)=100-x,
EF=OF-OE=(OA+![]() AB)-OE=(20+30)--
AB)-OE=(20+30)-- ![]() =50-
=50- ![]() ,
,
∴![]() =
=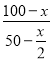 =2.
=2.

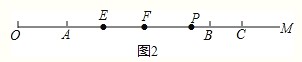
如图2,设OP=xcm,点P在线段AB上,20≤x≤80,OB-AP=80-(x-20)=100-x,
EF=OF-OE=(OA+![]() AB)-OE=(20+30)--
AB)-OE=(20+30)-- ![]() =50-
=50- ![]() ,
,
∴![]() =
=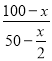 =2.
=2.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=2(x﹣1)2+k的图象上有三点A(﹣1,y1),B(2,y2),C(5,y3),则y1,y2,y3的大小关系为( )
A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y1<y2<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水300吨,计划内用水每吨收费3. 4元,超计划部分每吨按4. 6元收费.
(1)用代数式表示(所填结果需化简):
设用水量为![]() 吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.
吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.
(2)若某单位4月份缴纳水费1480元,则该单位用水多少吨?
(3)若某单位5、6月份共用水700吨(6月份用水量超过5月份),共交水费2560元,则该单位5、6月份各用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.

(1)求证:FD2=FB·FC.
(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AB=4,E是线段AC上的任意一点,∠BAC的平分线交BC于D,AD=2 ![]() ,F是AD上的动点,连接CF、EF,则CF+EF的最小值为 .
,F是AD上的动点,连接CF、EF,则CF+EF的最小值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com