

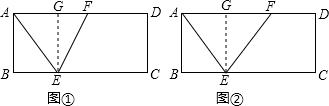
 解:如图,过点E作EG⊥AD于G,
解:如图,过点E作EG⊥AD于G,| 52-42 |
| 42+22 |
| 5 |
| 5 |


科目:初中数学 来源: 题型:
 某小区想借助如图所示的直角墙角(两足够长),用32米长的篱笆围成一个矩形花园ABCD(篱笆AB、BC两边),设AB=x米.
某小区想借助如图所示的直角墙角(两足够长),用32米长的篱笆围成一个矩形花园ABCD(篱笆AB、BC两边),设AB=x米.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )| A、α=β |
| B、α=2β |
| C、α+β=90° |
| D、α+2β=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,观察海岛(AB),立两标杆(CD,EF),并使点F,D,B在同一直线上,两标杆前后相距1000步,标杆均高3丈,若从标杆CD后退123步,观察者的眼睛H(靠近地面)与标杆顶端C,岛的峰顶A在同一直线上;从标杆EF后退127步,同样观察者的眼睛K(靠近地面)与标杆顶端E,岛的峰顶A在同一直线上;问海岛的峰高AB和海岛离标杆CD的距离BD分别为多少?(注:1步=6尺,1丈=10尺)
如图,观察海岛(AB),立两标杆(CD,EF),并使点F,D,B在同一直线上,两标杆前后相距1000步,标杆均高3丈,若从标杆CD后退123步,观察者的眼睛H(靠近地面)与标杆顶端C,岛的峰顶A在同一直线上;从标杆EF后退127步,同样观察者的眼睛K(靠近地面)与标杆顶端E,岛的峰顶A在同一直线上;问海岛的峰高AB和海岛离标杆CD的距离BD分别为多少?(注:1步=6尺,1丈=10尺)查看答案和解析>>
科目:初中数学 来源: 题型:
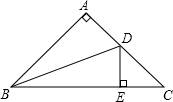 如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,若△DEC的周长是10cm,则BC=( )
如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,若△DEC的周长是10cm,则BC=( )| A、8cm | B、10cm |
| C、11cm | D、12cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com