Question

【题目】如图所示，在长方形ABCD中，AB＝8，BC＝4，将长方形沿AC折叠，使点D落在点D′处，求重叠部分△AFC的面积．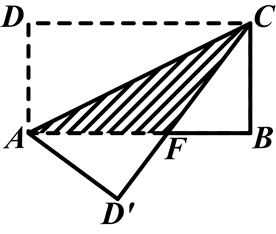

Answer 1

【答案】解：在长方形ABCD中，
∵AB∥CD，
∴∠BAC＝∠DCA．
又由折叠的性质可得∠DCA＝∠FCA．
∴∠BAC＝∠FCA．
∴AF＝CF．
设AF＝x，则BF＝AB－AF＝8－x．
在Rt△BCF中，BC＝4，BF＝8－x，CF＝x，
∴42＋(8－x)2＝x2 ． 解得x＝5．
∴ ．
【解析】由矩形性质得到∠BAC＝∠DCA；由折叠的性质得∠DCA＝∠FCA；根据等量代换可得∠BAC＝∠FCA；由等边对等角得AF＝CF．设AF＝x，则BF＝AB－AF＝8－x．在Rt△BCF中，由勾股定理得到一个一元二次方程，42＋(8－x)2＝x2 ． 解得x＝5．再由三角形面积公式即可求得。
【考点精析】本题主要考查了三角形的面积和勾股定理的概念的相关知识点，需要掌握三角形的面积=1/2×底×高；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．