
【题目】如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是

A. (-4,2) B. (-4.5,2) C. (-5,2) D. (-5.5,2 )
【答案】A
【解析】试题分析:因为⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(﹣1,2),则点Q的坐纵标是2,设PQ=2x,作MA⊥PQ,利用垂径定理可求QA=PA=x,连接MP,则MP=MO=x+1,在Rt△AMP中,利用勾股定理即可求出x的值,从而求出Q的横坐标=﹣(2x+1).
解:∵⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,点P的坐标是(﹣1,2)
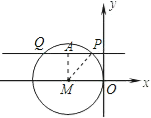
∴点Q的纵坐标是2
设PQ=2x,作MA⊥PQ,
利用垂径定理可知QA=PA=x,
连接MP,则MP=MO=x+1,
在Rt△AMP中,MA2+AP2=MP2
∴22+x2=(x+1)2∴x=1.5
∴PQ=3,Q的横坐标=﹣(1+3)=﹣4
∴Q(﹣4,2)
故选:A.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】为了调查红旗小学六年级学生的兴趣爱好,以下样本最具代表性的是( )
A. 该年级书法社团的学生 B. 该年级部分女学生
C. 该年级跑步较快的学生 D. 从每个班级中,抽取学号为10的整数倍的学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内有2014条直线a1,a2,…,a2014,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,依此类推,那么a1与a2014的位置关系是( )
A. 垂直
B. 平行
C. 垂直或平行
D. 重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A.36(1﹣x)2=36﹣25
B.36(1﹣2x)=25
C.36(1﹣x)2=25
D.36(1﹣x2)=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市按以下规定收取每月的水费:用水不超过10立方米,按每立方米2.1元收费;如果超过10立方米,超过部分按每立方米3元收费,已知某用户l2月水费平均每立方米2.5元.
按要求回答下列问题:
(1)这个用户12月用水量10立方米(填“超过”或“不超过”).
(2)在(1)的前提下,求12月这个用户的用水量是多少立方米?
(3)该用户12月份需交水费元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图。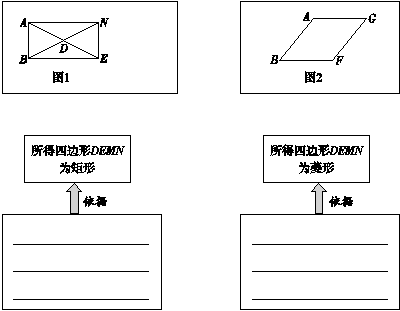
(1)画图-连线-写依据:
先分别完成以下画图(不要求尺规作图),再与判断四边形DEMN形状的相应结论连线,并写出判定依据(只将最后一步判定特殊平行四边形的依据填在横线上).
①如图1,在矩形ABEN中,D为对角线的交点,过点N画直线NP∥DE , 过点E画直线EQ∥DN , NP与EQ的交点为点M , 得到四边形DEMN;
②如图2,在菱形ABFG中,顺次连接四边AB , BF , FG , GA的中点D , E , M , N , 得到四边形DEMN.
(2)请从图1、图2的结论中选择一个进行证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com