Question

【题目】如下图。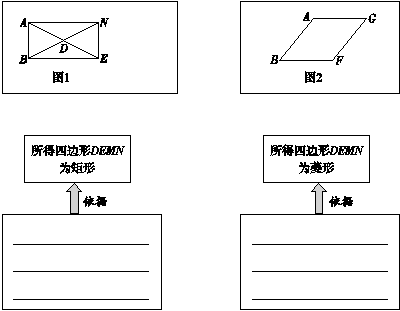

（1）画图－连线－写依据：
先分别完成以下画图（不要求尺规作图），再与判断四边形DEMN形状的相应结论连线，并写出判定依据（只将最后一步判定特殊平行四边形的依据填在横线上）.
①如图1，在矩形ABEN中，D为对角线的交点，过点N画直线NP∥DE ， 过点E画直线EQ∥DN ， NP与EQ的交点为点M ， 得到四边形DEMN；
②如图2，在菱形ABFG中，顺次连接四边AB ， BF ， FG ， GA的中点D ， E ， M ， N ， 得到四边形DEMN.
（2）请从图1、图2的结论中选择一个进行证明.

Answer 1

【答案】
（1）

解：见图3，图4，连线、

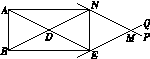
图3依据：有一组邻边相等的平行四边形为菱形.

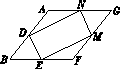
图4依据：有一个角为直角的平行四边形为矩形.

（2）

证明：①如图3.

∵ NP∥DE，EQ∥DN，NP与EQ的交点为点M，

∴ 四边形DEMN为平行四边形.

∵ D为矩形ABEN对角线的交点，

∴ AE=BN， ， .

∴ DE= DN.

∴ 平行四边形DEMN是菱形.

②如图5，连接AF，BG，记交点为H.

∵ D，N两点分别为AB，GA边的中点，

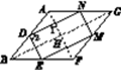
图5

∴ DN∥BG， .

同理，EM∥BG， ，DE∥AF， .

∴ DN∥EM，DN=EM.

∴ 四边形DEMN为平行四边形.

∵ 四边形ABFG是菱形，

∴ AF⊥BG.

∴ .

∴ .

∴ .

∴ 平行四边形DEMN是矩形

【解析】（1）如图3，依据为有一组邻边相等的平行四边形为菱形.如图4依据为有一个角为直角的平行四边形为矩形.
（2）①如图3.由NP∥DE，EQ∥DN得 四边形DEMN为平行四边形；根据DE= DN得到平行四边形DEMN是菱形.
②如图5，连接AF ， BG ， 记交点为H.由 D ， N、E、M为中点得DN∥EM ， DN=EM.所以四边形DEMN为平行四边形.由菱形得 =
所以 平行四边形DEMN是矩形。