
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:填空题
| 编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ |
| 原来球队 | 72 | 72 | 77 | 77 | 78 | 80 | 86 | 86 | 92 |
| 现在球队 | 72 | 72 | 77 | 77 | 78 | 93 | 84 | 83 | 84 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
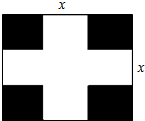 为了美化校园,学校在校内一块长30m,宽20m的长方形空地上修建如图所示的十字路(空白处),四个角铺上草坪(面积相等的小长方形的阴影部分).设十字路的宽为xm,则用整式表示草坪的面积为600-50x+x2m2.
为了美化校园,学校在校内一块长30m,宽20m的长方形空地上修建如图所示的十字路(空白处),四个角铺上草坪(面积相等的小长方形的阴影部分).设十字路的宽为xm,则用整式表示草坪的面积为600-50x+x2m2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com