
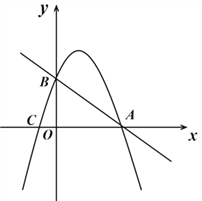
【题目】已知,如图,抛物线y = ax2 + bx + c![]() 交x轴于A(4,0),C(-1,0)两点,交y轴于点B(0,3) .
交x轴于A(4,0),C(-1,0)两点,交y轴于点B(0,3) .
(1)求抛物线y = ax2 + bx + c![]() 的解析式;
的解析式;
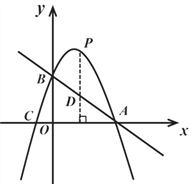
(2)点P是抛物线(在点A与点B之间的部分)上的点,求△ABP的面积最大值;
(3)若点M在y轴上,且△ABM为等腰三角形,请直接写出M点坐标.
【答案】(1) ![]() ; (2)6;(3) M坐标为(0,8)或 (0,-2) 或(0,-3) 或(0,
; (2)6;(3) M坐标为(0,8)或 (0,-2) 或(0,-3) 或(0,![]() ).
).
【解析】分析:![]() 用待定系数法确定函数关系式即可.
用待定系数法确定函数关系式即可.
![]() 用待定系数法求出直线
用待定系数法求出直线![]() 的解析式,设点P的横坐标为m,作PD⊥x轴交AB于点D,表示出△ABP的面积,根据二次函数的性质即可求出最大值.
的解析式,设点P的横坐标为m,作PD⊥x轴交AB于点D,表示出△ABP的面积,根据二次函数的性质即可求出最大值.
![]() 分三种情况进行讨论:
分三种情况进行讨论:![]()
详解:(1)将A(4,0)、 B(0,3)、C(-1,0)代入得
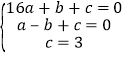 ,解得
,解得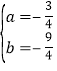 ,∴
,∴![]() .
.
(2)设直线AB为y1=k1x+b,将A(4,0), B(0,3)代入得
![]() ,解得
,解得![]() ,∴
,∴![]() .
.
设点P的横坐标为m,作PD⊥x轴交AB于点D,
∴![]() ,
,
∴S△PBA=![]() OAPD=
OAPD=![]() ×4×(
×4×(![]() )=
)=![]() ,
,
∴S△PBA的最大值 = 6,
(3)点M坐标为(0,8)或 (0,-2) 或(0,-3) 或(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某市交警大队一辆警车每天在一段东西方向的公路上巡逻执法.一天上午从![]() 地出发,中午到达
地出发,中午到达![]() 地,规定向东行驶的里程为正,向西行驶的里程为负,这天行驶的里程数记录如下(单位:
地,规定向东行驶的里程为正,向西行驶的里程为负,这天行驶的里程数记录如下(单位:![]() );
);![]() ,
,
(1)问![]() 地在
地在![]() 地的东面还是西面?
地的东面还是西面?![]() ,
,![]() 两地相距多少千米?
两地相距多少千米?
(2)若该警车每千米耗油![]() 升,警车出发时,油箱中有油
升,警车出发时,油箱中有油![]() 升,请问中途有没有给警车加过油?若有,至少加了多少升油?请说明理由.
升,请问中途有没有给警车加过油?若有,至少加了多少升油?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你喜欢玩游戏吗?现请你玩一个转盘游戏.如图所示的两上转盘中指针落在每一个数字上的机会均等,现同时自由转动甲、乙两个转盘,转盘停止后,指针各指向一个数字,用所指的两个数字作乘积.所有可能得到的不同的积分别为_______________________;数字之积为奇数的概率为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列现象中,与“把弯曲的公路改直,就能缩短路程”原理一致的是( )
A.从![]() 地到
地到![]() 地架设电线,总是尽可能沿着线段
地架设电线,总是尽可能沿着线段![]() 架设
架设
B.植树时,只要定出两棵树的位置,就能确定所植树木是否成行
C.用两个钉子就可以把木条固定在墙上
D.体育老师画直线跑道时,常把一根长线的两端系在标枪上,插到欲画跑道两端并拉紧,得到一条参照线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是![]() ,且
,且![]() ,则CD=( )
,则CD=( )

A.2.5ABB.3ABC.3.5ABD.4AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E为AD上一点,BE ⊥ AC于F点.

(1)若AE=![]() AD,△AEF的面积为1时,求△ABC的面积;
AD,△AEF的面积为1时,求△ABC的面积;
(2)若AD = 4,tan∠EAF =![]() ,求AF的长;
,求AF的长;
(3)若tan∠EAF =![]() ,连接DF,证明DF=AB.
,连接DF,证明DF=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一些数学问题的研究可以经历观察、探究、发现、证明等过程.下面是对一个问题的部分研究过程:
(观察)![]() =
=![]() ,
,![]() =
=![]() ,
,![]() 是否也能写成分数的形式?
是否也能写成分数的形式?
(探究1)设![]() =x,
=x,
由![]() =0.555…可知,10x=5.555…,
=0.555…可知,10x=5.555…,
所以10x﹣x=5.
解方程,得x=![]()
于是,得![]() =
=![]() .
.
所以,![]() 能写成分数的形式
能写成分数的形式
(探究2)仿照上面的方法,尝试将![]() 写成分数的形式.
写成分数的形式.
(发现) .
请你完成(探究2)的部分,并用一句话概括你的发现
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com