
【题目】按要求解答下列各题
(1)已知a、b 互为相反数,c、d 互为倒数,x=(-2)2。
试求x2 -(a + b + c×d) x +(a + b)2015 +(-c×d)2016的值。
(2)已知有理数a、b、c 满足|a-1|+|b-3|+|3c-1|=0,求(a×b×c)178 ÷(a36×b7×c6)的值。
【答案】(1)13 (2)![]()
【解析】
(1)由已知可得a+b=0,cd=1,x=4,再代入原式可得;(2)由非负数性质得a-1=0,b-3=0,3c-1=0.求出a,b,c,再代入求值.
解:(1)因为a、b 互为相反数,c、d 互为倒数,x=(-2)2
所以,a+b=0,cd=1,x=4,
所以,x2 -(a + b + c×d) x +(a + b)2015 +(-c×d)2016
=42-(0+1)×4+02015+(-1)2016
=16-4+0+1
=13.
(2)因为|a-1|+|b-3|+|3c-1|=0,
所以,根据非负数性质得:a-1=0,b-3=0,3c-1=0.
所以,a=1,b=3,c=![]() ,
,
所以,(a×b×c)178 ÷(a36×b7×c6)
=(1×3×![]() )178 ÷[136×37×(
)178 ÷[136×37×(![]() )6]
)6]
=1÷3
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于点C,O是坐标原点,已知点B的坐标是(3,0),tan∠OAC=3;
(1)求该抛物线的函数表达式;
(2)点P在x轴上方的抛物线上,且∠PAB=∠CAB,求点P的坐标;
(3)若平行于x轴的直线与抛物线交于点M、N(M点在N点左侧),
①若以MN为直径的圆与x轴相切,求该圆的半径;
②若Q(m,4)是直线MN上一动点,当以点C、B、Q为顶点的三角形的面积等于6时,请直接写出符合条件的m值,为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解学生“自主学习、合作交流”的情况,对八年级各班部分同学进行了一段时间的跟踪调査,将调查结果(A:特别好; B:较好; C:一般; D:较差)绘制成以下两幅不完整的统计图. 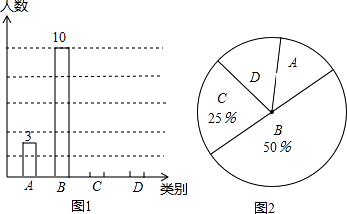
请根据图中提供的信息,解答下列问题:
(1)此次跟踪调查的学生有人;扇形统计图中,D类所占圆心角为度;
(2)补全条形统计图;
(3)如果该校八年级共有学生360人,试估计A类学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小英在周末和爸爸妈妈以及爷爷奶奶一行6人,自驾外出旅游,出发前油箱里有油5升,在加油站加140元的油.已知油价是7元/升,目的地距离出发地320千米,正常行驶时,车子的耗油情况是0.42元/千米.
(1)在加油站加油 升;车子的耗油情况换算成 升/千米.
(2)在行驶过程中,设油箱内余油y(升),行驶路程x(千米),将y表示为x的函数.
(3)若油箱里余油量低于5升会自动报警,通过计算回答,小明他们在到达目的地之前,车子是否会自动报警.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个数用大括号括起来,中间用逗号断开,如:{1,2,-3},{-2,7,![]() ,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{5,0}就是一个好的集合.
,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{5,0}就是一个好的集合.
(1)请你判断集合{1,2},{-2,1,2.5,4,7}是不是好的集合?
(2)请你再写出两个好的集合(不得与上面出现过的集合重复);
(3)写出所有好的集合中,元素个数最少的集合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴负半轴交于点A(﹣1,0),与y轴正半轴交于点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
(1)求一次函数解析式;
(2)求顶点P的坐标;
(3)平移直线AB使其过点P,如果点M在平移后的直线上,且 ![]() ,求点M坐标;
,求点M坐标;
(4)设抛物线的对称轴交x轴于点E,连接AP交y轴于点D,若点Q、N分别为两线段PE、PD上的动点,连接QD、QN,请直接写出QD+QN的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com