
分析 由于1+2+…+n=$\frac{n(n+1)}{2}$,那么$\frac{1}{1+2+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),依此可得原式=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{10}$-$\frac{1}{11}$)=$\frac{20}{11}$.
解答 解:原式=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{10}$-$\frac{1}{11}$)
=2(1-$\frac{1}{11}$)
=$\frac{20}{11}$.
故答案为$\frac{20}{11}$.
点评 本题考查了规律型:数字的变化类,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.解决本题的难点在于找到规律:$\frac{1}{1+2+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$).


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
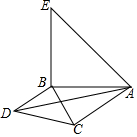 已知,如图,在△ABC中,∠BAC=45°,以B为直角顶点分别作Rt△BCD、Rt△BAE,且BC=BD,BA=BE,连接AD.猜想并证明线段AB、AD、AC之间的数量关系.
已知,如图,在△ABC中,∠BAC=45°,以B为直角顶点分别作Rt△BCD、Rt△BAE,且BC=BD,BA=BE,连接AD.猜想并证明线段AB、AD、AC之间的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )| A. | 135° | B. | 125° | C. | 90° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12π cm2 | B. | 15π cm2 | C. | 20π cm2 | D. | 25π cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O是四边形ABCD的外接圆,AB是⊙O的直径,BC=CD,过点C作PM⊥AD交AD的延长线于点M,交AB的延长线于点P.
如图,已知⊙O是四边形ABCD的外接圆,AB是⊙O的直径,BC=CD,过点C作PM⊥AD交AD的延长线于点M,交AB的延长线于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com