
����Ŀ����������Сѧ�����ҵ��й��Ρ������У�ijУ�Բ���ѧ������һ������Ϊ������ϲ����ͼ�顱�ĵ�������ͼ���Ϊ�ס��ҡ����������࣬ѧ���ɸ����Լ��İ�����ѡ����һ�࣮ѧУ���ݵ������������ͳ�ƣ��������˲�����������ͳ��ͼ������ͳ��ͼ�� 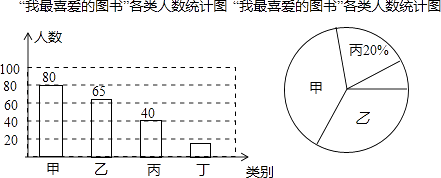
������ͼ����Ϣ������������⣨���У�1������2��ֱ����𰸼��ɣ���
��1�����ι���������ѧ����
��2���������ѧ���У���ϲ������ͼ���ѧ�����ˣ���ϲ������ͼ�������ռ���α�����������%��
��3������ϲ������ͼ���ѧ���У�Ů������������������1.5����������ѧУ����ѧ��2000�ˣ�������Ƹ�У��ϲ������ͼ���Ů���������ֱ��ж����ˣ�
���𰸡�
��1��200
��2��15��40
��3���⣺���У��ϲ������ͼ���Ů���������ֱ�1.5x�ˣ�x�ˣ�
���������г����̵ã�x+1.5x=2000��20%��
��ã�x=160��
��ʱ1.5x=240��
���У��ϲ������ͼ���Ů���������ֱ�Ϊ240�ˣ�160��
���������⣺��1����������ã�40��20%=200��������
�ʴ�Ϊ��200����2����������ã�����ѧ����Ϊ200����80+65+40��=15��������
��ϲ������ͼ�������ռ���α����������İٷֱ�= ![]() ��100%=40%��
��100%=40%��
�ʴ�Ϊ��15��40��
��1�����ݱ���Ӧ�������Լ��ٷֱȣ����ɵõ��������������2������200����80+65+40�����м��㣬���ɵõ�ϲ������ͼ���ѧ������������ϲ������ͼ����������������������ɵõ���ϲ������ͼ�������ռ���α����������İٷ�������3�����У��ϲ������ͼ���Ů���������ֱ�1.5x�ˣ�x�ˣ��ٸ��������г����̵ã�x+1.5x=2000��20%�������õ���У��ϲ������ͼ���Ů����������������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AB��BC��CD��DE��EA��ɵ�ƽ��ͼ�Σ����1+��2+��3+��4+��5= �� 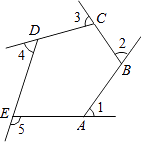
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ɡ�A��B��C����O����ת180����õ��������н��۲��������ǣ� ��
A.��A���A���Ƕ�Ӧ��
B.BO=B��O
C.��ACB=��C��A��B��
D.AB��A��B��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���ABC=90�㣬AB=BC�������εĶ������ƽ�е�����ֱ��l1 �� l2 �� l3�ϣ���l1 �� l2֮��ľ���Ϊ2��l2 �� l3֮��ľ���Ϊ3����AC�ij��ǣ� �� 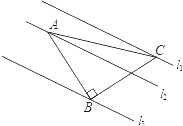
A.![]()
B.![]()
C.![]()
D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ˮ�շ�ʵ�н���ˮ�ۣ��շѱ����±���ʾ��
��1��ij�û����·���ˮ��Ϊ16�֣��轻ˮ��Ϊ����Ԫ��
��2��ij�û����·ݽ�ˮ��50Ԫ������ˮ��Ϊ���ٶ֣�
��3��ij�û����·���ˮ��Ϊa�֣���Ҫ��ˮ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��ֱ��l��һ�㣬��A��B��C��D��ֱ��l�ϵĵ㣬����PA��PB��PC��PD������ֻ��PA��l��ֱ����PA��7��PB��8��PC��10��PD��14�����P��ֱ��l�ľ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A����1��0����C��1��4������B��x���ϣ���AB=4��
��1�����B�����ꣻ
��2�����ABC�������
��3����y�����Ƿ���ڵ�P��ʹ��A��B��P����Ϊ����������ε����Ϊ7�������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��y�Ķ�Ԫһ�η����� ![]() �ĽⶼΪ������
�ĽⶼΪ������
��1����a��ȡֵ��Χ��
��2������|a+1|��|a��1|��
��3����������Ԫһ�η�����Ľ���һ�����������ε�һ������һ���ױߵij�����������������ε��ܳ�Ϊ9����a��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com