
【题目】如图,在△ABC中,点D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于点E.

(1)若∠A=80°,求∠BDC的度数;
(2)若∠EDC=40°,求∠A的度数;
(3)请直接写出∠A与∠BDC之间的数量关系(不必说明理由).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,点E,F,G分别是等边三角形ABC三边AB,BC,CA上的动点,且始终保持AE=BF=CG,设△EFG的面积为y,AE的长为x,y关于x的函数图象大致为图2所示,则等边三角形ABC的边长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图像如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:

(1)ac>0;
(2)方程ax2+bx+c=0的两根是x1=-1,x2=3;
(3)2a-b=0;
(4)当x>1时,y随x的增大而减小;
(5)3a+2b+c>0
则以上结论中不正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.

【答案】(1)5.6m;(2)应挪走.
【解析】试题解析:试题分析:(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
试题解析:(1)如图,
在Rt△ABD中,AD=ABsin45°=4![]() .
.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走.
解:在Rt△ABD中,BD=ABcos45°=4![]() =4.
=4.
在Rt△ACD中,CD=![]() AD=4
AD=4![]() .
.
∴CB=CD-BD=4![]() -4≈2.8.
-4≈2.8.
∵PC=PB-CB≈5-2.8=2.2>2,
∴货物MNQP不应挪走.
【题型】解答题
【结束】
8
【题目】如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。
(1)求该圆锥形粮堆的侧面积。
(2)母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。 (结果不取近似数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在全省各大景区都在流行“真人CS“娱乐项目,其中有一个“快速抢点”游戏,游戏规则:如图,用绳子围成的一个边长为10m的正方形ABCD场地中,游戏者从AB边上的点E处出发,分别先后赶往边BC、CD、DA上插小旗子,最后回到点![]() 已知
已知![]() ,则游戏者所跑的最少路程是多少______
,则游戏者所跑的最少路程是多少______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数” .将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123) =6.
(1)计算:F(315),F(746);
(2)若s、t都是“相异数”,其中s=100x+42,t=160+y(1≤x≤9,1≤y≤9,x、y都是正整数),当F(s)+F(t)=17时,求x、y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示:

设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
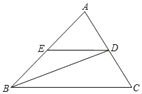
【题目】如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创造了一幅“弦图”后人称其为“赵爽弦图”(如图1).图2是弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,求S2的值.以下是求S2的值的解题过程,请你根据图形补充完整.
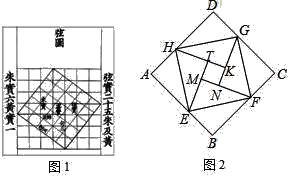
解:设每个直角三角形的面积为S
S1﹣S2= (用含S的代数式表示)①
S2﹣S3= (用含S的代数式表示)②
由①,②得,S1+S3= 因为S1+S2+S3=10,
所以2S2+S2=10.
所以S2=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com