
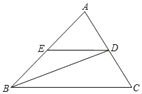
【题目】如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.
【答案】(1)证明见解析;(2)25°.
【解析】
(1)由等腰三角形的性质可得∠C=∠A,由平行线的性质可得∠C=∠ADE,从而∠A=∠ADE;
(2)先由三角形内角和求出∠ABC=50°,再由三线合一的性质可求出∠EBD=∠DBC=![]() ∠ABC=25°,然后根据平行线的性质求解即可.
∠ABC=25°,然后根据平行线的性质求解即可.
证明:(1)∵DE∥BC,
∴∠C=∠ADE,
∵AB=BC,
∴∠C=∠A,
∴∠A=∠ADE,
∴AE=DE;
(2)∵△ABC中,AB=BC,∠C=65°,
∴∠ABC=180°﹣65°﹣65°=50°,
∵AB=BC,D为AC中点,
∴∠EBD=∠DBC=![]() ∠ABC=25°,
∠ABC=25°,
∵DE∥BC,
∴∠BDE=∠DBC=25°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于点E.

(1)若∠A=80°,求∠BDC的度数;
(2)若∠EDC=40°,求∠A的度数;
(3)请直接写出∠A与∠BDC之间的数量关系(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() =k(k为大于
=k(k为大于![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
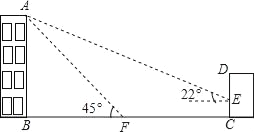
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上)
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
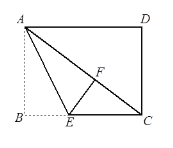
【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
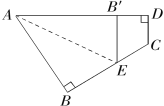
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=![]() ,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;并说明理由.
(2)如果∠C=![]() ,求∠AEB的度数.
,求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题:
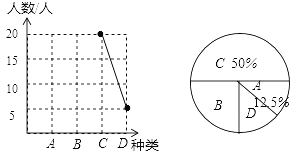
(1)请补全折线统计图,并求出“动漫潮”所在扇形的圆心角度数.
(2)据统计,在被调查的学生中,喜欢“文艺范”类型的仅有2名住读生,其余均为走读生,初二年级欲从喜欢“文艺范”的这几名同学中随机抽取两名同学去观摩“文明礼仪大赛”视频,用列表法或树状图的方法求出所选的两名同学都是走读生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com