
【题目】如图所示,A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____.

【答案】 AF=DE或∠E=∠F或BE∥CF
【解析】
本题要判定△ACF≌△DBE,由已知DE∥AF可得∠A=∠D,又有AC=BD,具备了一组角、一组边对应相等,然后根据全等三角形的判定定理,有针对性的添加条件.
解:添加AF=DE、∠E=∠F、BE∥CF、∠ACF=∠DBE后可分别根据SAS、AAS、ASA、ASA能判定△ACF≌△DBE.
故填AF=DE、∠E=∠F、BE∥CF、∠ACF=∠DBE等,答案不唯一.
考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关健.


科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(45°)是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D)在同一条直线上).请求出旗杆MN的高度.(参考数据:![]() ,
,![]() ,结果保留整数)
,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,可以单独用正三角形、正方形或正六边形铺满地面,如果我们要同时用两种不同的正多边形铺满地面,可以设计出几种不同的组合方案?
问题解决:
猜想1:是否可以同时用正方形、正八边形两种正多边形组合铺满地面?
验证1并完成填空:在铺地面时,设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意:可得方程①: ,
整理得②: ,
我们可以找到方程的正整数解为③: .
结论1:铺满地面时,在一个顶点周围围绕着④个正方形和⑤个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以铺满地面.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合铺满地面?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)与x轴一个交点在﹣1,﹣2之间,对称轴为直线x=1,图象如图,给出以下结论:①b2﹣4ac>0;②abc>0;③2a﹣b=0;④8a+c<0;⑤a+![]() b+
b+![]() c<0.其中结论正确的个数有( )
c<0.其中结论正确的个数有( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从A地出发,匀速开往B地.甲车行驶到B地后立即沿原路线以原速度返回A地,到达A地后停止运动;当甲车到达A地时,乙车恰好到达B地,并停止运动.已知甲车的速度为150km/h.设甲车出发xh后,甲、乙两车之间的距离为ykm,图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.
(1)A、B两地的距离是______km,乙车的速度是______km/h;
(2)指出点M的实际意义,并求线段MN所表示的y与x之间的函数表达式;
(3)当两车相距150km时,直接写出x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有 4 个红球和 6 个黄球,这些球除颜色外都相同,将袋子中的球充 分摇匀后,随机摸出一球.
(1)分别求摸出红球和摸出黄球的概率
(2)为了使摸出两种球的概率相同,再放进去 8 个同样的红球或黄球,那么这 8 个球中红球和 黄球的数量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
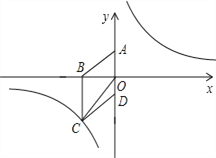
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且![]() (0,3)、
(0,3)、![]() (﹣4,0).
(﹣4,0).
(1)求经过点![]() 的反比例函数的解析式;
的反比例函数的解析式;
(2)设![]() 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以![]() 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com