
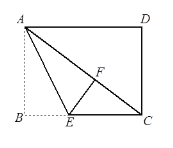
【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面鱼角坐标系xOy中,A(﹣3,0),点B为y轴正半轴上一点,将线段AB绕点B旋转90°至BC处,过点C作CD垂直x轴于点D,若四边形ABCD的面积为36,则线AC的解析式为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数” .将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123) =6.
(1)计算:F(315),F(746);
(2)若s、t都是“相异数”,其中s=100x+42,t=160+y(1≤x≤9,1≤y≤9,x、y都是正整数),当F(s)+F(t)=17时,求x、y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第2个正方形A1B1C1C;延长C1B1交x轴于点A2,作第3个正方形A2B2C2C1…按这样的规律进行下去,第2个正方形的面积为_____;第2011个正方形的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
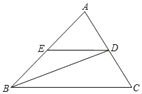
【题目】如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x![]() -ax+a
-ax+a![]() -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
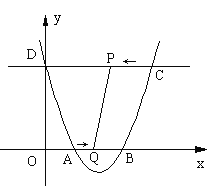
(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
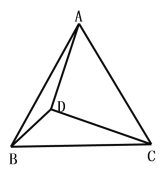
【题目】已知:△ABC为等边三角形
(1)若D为△ABC外一点,满足∠CDB=30,求证:![]()
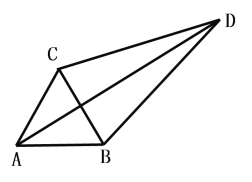
(2)若D为△ABC内一点,DC=3,DB=4,DA=5,求∠CDB的度数
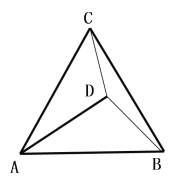
(3)若D为△ABC内一点,DA=4,DB=![]() ,DC=
,DC=![]() 则AB= (直接写出答案)
则AB= (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.
(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,调查方式选择最合理的是![]()
![]()
A. 为了解安徽省中学生的课外阅读情况,选择全面调查
B. 调查七年级某班学生打网络游戏的情况,选择抽样调查
C. 为确保长征六号遥二火箭成功发射,应对零部件进行全面调查
D. 为了解一批袋装食品是否含有防腐剂,选择全面调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com