
【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数” .将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123) =6.
(1)计算:F(315),F(746);
(2)若s、t都是“相异数”,其中s=100x+42,t=160+y(1≤x≤9,1≤y≤9,x、y都是正整数),当F(s)+F(t)=17时,求x、y的值.
【答案】(1)9 17 (2)![]()
【解析】
(1)根据相异数的概念首先写出对调的三个数,再求和,计算F(315),F(746)即可;
(2)首先根据题意计算F(s)和F(t),求解x和y的值即可.
(1)根据题意可得315的三个数的和为:315+531+153=999
所以999÷111=9
故F(315)=9
746的三个三位数的和为:746+674+467=1887
所以1887÷111=17
故F(746)=17
(2)![]() s、t都是相异数,s=100x+42, t=160+y
s、t都是相异数,s=100x+42, t=160+y
![]() F(s)=(100x+42+420+x+204+10x)÷111=x+6
F(s)=(100x+42+420+x+204+10x)÷111=x+6
F(t)=(160+y+601+10y+100y+16) ÷111=y+7
![]() F(s)+F(t)=17
F(s)+F(t)=17
![]()
![]()
![]() x+y=4
x+y=4
![]() 1≤x≤9,1≤y≤9,x、y都是正整数
1≤x≤9,1≤y≤9,x、y都是正整数
![]() 或
或![]() 或
或![]()
![]() s和t都是相异数
s和t都是相异数
![]() ,
,![]()
![]()


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】探寻“勾股数”:直角三角形三边长是整数时我们称之为“勾股数”,勾股数有多少?勾股数有规律吗?
(1)请你写出两组勾股数.
(2)试构造勾股数.构造勾股数就是要寻找3个正整数,使他们满足“两个数的平方和(或差)等于第三数的平方”,即满足以下形式:
① 2+ 2= 2;或② 2﹣ 2= 2
③要满足以上①、②的形式,不妨从乘法公式入手.我们已经知道③(x+y)2﹣(x﹣y)2=4xy.如果等式③右边也能写成 2的形式,就能符合②的形式.
因此不妨设x=m2,y=n2,(m、n为任意正整数,m>n),请你写出含m、n的这三个勾股数并证明它们是勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ![]() ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( )

A. 1+3![]() B. 3+
B. 3+![]() C. 4+
C. 4+![]() D. 5+
D. 5+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于点E.

(1)若∠A=80°,求∠BDC的度数;
(2)若∠EDC=40°,求∠A的度数;
(3)请直接写出∠A与∠BDC之间的数量关系(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
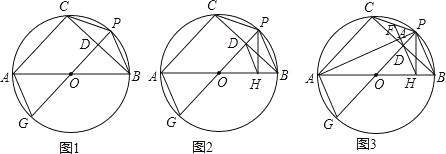
【题目】⊙O是△ABC的外接圆,AB是直径,过![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() =k(k为大于
=k(k为大于![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
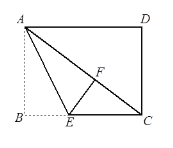
【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com