
【题目】在平面直角坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第2个正方形A1B1C1C;延长C1B1交x轴于点A2,作第3个正方形A2B2C2C1…按这样的规律进行下去,第2个正方形的面积为_____;第2011个正方形的面积为_____.

【答案】![]() 5×
5×![]()
【解析】
推出AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,求出∠ADO=∠BAA1,证△DOA∽△ABA1,得出![]() ,求出AB,BA1,求出边长A1C=
,求出AB,BA1,求出边长A1C=![]() ,求出面积即可;求出第3个正方形的边长是
,求出面积即可;求出第3个正方形的边长是![]() ,面积
,面积![]() ;第4个正方形的面积是
;第4个正方形的面积是![]() ×
×![]() ;依此类推得出第2011个正方形的边长是
;依此类推得出第2011个正方形的边长是![]()
![]() ,面积是
,面积是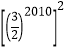 ×
×![]() ,即可得出答案.
,即可得出答案.
解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,
∴∠ADO+∠DAO=90°,∠DAO+∠BAA1=90°,
∴∠ADO=∠BAA1,
∵∠DOA=∠ABA1,
∴△DOA∽△ABA1,
∴![]() ,
,
∵AB=AD=![]() =
=![]() ,
,
∴BA1=![]()
![]() ,
,
∴第2个正方形A1B1C1C的边长A1C=A1B+BC=![]()
![]() ,面积是
,面积是![]() =
=![]() ×
×![]() =
=![]() ×5=
×5=![]() ;
;
同理第3个正方形的边长是![]() +
+![]() =
=![]() =
=![]()
![]() ,面积是:
,面积是:![]() =
=![]() ;
;
第4个正方形的边长是![]()
![]() ,面积是[
,面积是[![]() ]2×
]2×![]() ;
;
…
第2011个正方形的边长是![]()
![]() ,面积是
,面积是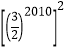 ×
×![]() =5×
=5×![]() .
.
故答案为:![]() ,5×
,5×![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
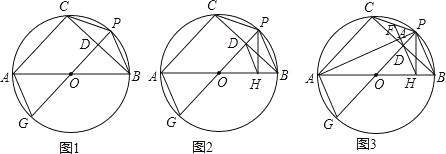
【题目】⊙O是△ABC的外接圆,AB是直径,过![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() =k(k为大于
=k(k为大于![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
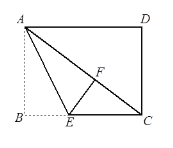
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y=![]() 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的菱形ABCD纸片放置在平面直角坐标系中.已知∠ABO=45°.
的菱形ABCD纸片放置在平面直角坐标系中.已知∠ABO=45°.
(1)求出点B、C的坐标;
(2)设边AB沿y轴对折后的对应线段为AB′,求出点B′的坐标及线段CB′的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com