
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2-4x+3.(2)当m=![]() 时,四边形AOPE面积最大,最大值为
时,四边形AOPE面积最大,最大值为![]() .(3)P点的坐标为 :P1(
.(3)P点的坐标为 :P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】
(1)利用对称性可得点D的坐标,利用交点式可得抛物线的解析式;
(2)设P(m,m2-4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得四边形AOPE的面积,利用配方法可得其最大值;
(3)存在四种情况:
如图3,作辅助线,构建全等三角形,证明△OMP≌△PNF,根据OM=PN列方程可得点P的坐标;同理可得其他图形中点P的坐标.
(1)如图1,设抛物线与x轴的另一个交点为D,
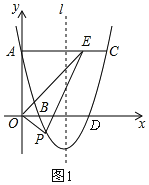
由对称性得:D(3,0),
设抛物线的解析式为:y=a(x-1)(x-3),
把A(0,3)代入得:3=3a,
a=1,
∴抛物线的解析式;y=x2-4x+3;
(2)如图2,设P(m,m2-4m+3),
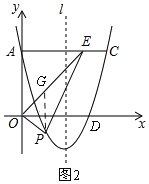
∵OE平分∠AOB,∠AOB=90°,
∴∠AOE=45°,
∴△AOE是等腰直角三角形,
∴AE=OA=3,
∴E(3,3),
易得OE的解析式为:y=x,
过P作PG∥y轴,交OE于点G,
∴G(m,m),
∴PG=m-(m2-4m+3)=-m2+5m-3,
∴S四边形AOPE=S△AOE+S△POE,
=![]() ×3×3+
×3×3+![]() PGAE,
PGAE,
=![]() +
+![]() ×3×(-m2+5m-3),
×3×(-m2+5m-3),
=-![]() m2+
m2+![]() m,
m,
=![]() (m-
(m-![]() ,
,
∵-![]() <0,
<0,
∴当m=![]() 时,S有最大值是
时,S有最大值是![]() ;
;
(3)如图3,过P作MN⊥y轴,交y轴于M,交l于N,
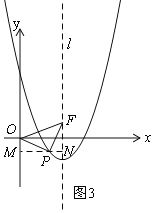
∵△OPF是等腰直角三角形,且OP=PF,
易得△OMP≌△PNF,
∴OM=PN,
∵P(m,m2-4m+3),
则-m2+4m-3=2-m,
解得:m=![]() 或
或![]() ,
,
∴P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
如图4,过P作MN⊥x轴于N,过F作FM⊥MN于M,
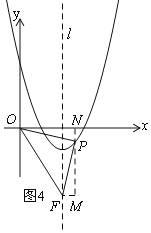
同理得△ONP≌△PMF,
∴PN=FM,
则-m2+4m-3=m-2,
解得:x=![]() 或
或![]() ;
;
P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上所述,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】计算:
①8+(﹣10)+(﹣2)﹣(﹣5)
②2![]() ﹣3
﹣3![]() ﹣5
﹣5![]() ﹣|﹣3
﹣|﹣3![]() |
|
③(﹣1![]() )+1.25+(﹣8.5)+10
)+1.25+(﹣8.5)+10![]()
④(![]() )×(﹣12)
)×(﹣12)
⑤(﹣199![]() )×5(用简便方法计算)
)×5(用简便方法计算)
⑥10×(﹣![]() )﹣2×
)﹣2×![]() +(﹣3)×(﹣
+(﹣3)×(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
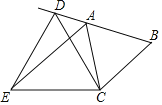
【题目】如图,等边△ABC的边长为4,D是线段BA延长线上的一点,以线段CD为边向CD的左侧作等边△CDE,连接AE.
(1)△ABC的面积S△ABC= ;
(2)求证:△ACE≌△BCD;
(3)若四边形ABCE的面积为10![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,小明在书店停留了 分钟
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟.
(3)我们认为骑单车的速度超过300米分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC 的顶点 A (-2,0),点 B,C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°
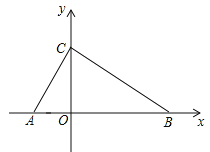
(1)求点 B 的坐标;
(2)点 P 为 AC延长线上一点,过 P 作PQ∥x轴交 BC 的延长线于点 Q ,若点 P 的横坐标为t,线段PQ的长为d,请用含t的式子表示d;
(3) 在(2)的条件下,当PA=![]() d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机王师傅某天早上营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天早上所接六位乘客的行车里程(![]() )如下:
)如下:
2,+5,-4,+1,-6,-2
(1)将最后一位乘客送到目的地时,王师傅在早上出发点的什么位置?
(2)若汽车耗油量为![]() ,这天早上王师傅接送乘客,出租车共耗油多少升?
,这天早上王师傅接送乘客,出租车共耗油多少升?
(3)若出租车起步价为6元,起步里程为![]() (包括
(包括![]() ),超过部分(不足
),超过部分(不足![]() 按
按![]() 计算)每千米1.5元,王师傅这天早上共得车费多少元?
计算)每千米1.5元,王师傅这天早上共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
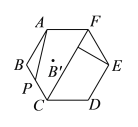
【题目】如图所示,正六边形![]() 的边长为
的边长为![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 运动至点
运动至点![]() ,点
,点![]() 是点
是点![]() 关于直线
关于直线![]() 对称的点.
对称的点.
(![]() )点
)点![]() 从点
从点![]() 运动至
运动至![]() 过程中,下列说法正确的有__________.(填序号)
过程中,下列说法正确的有__________.(填序号)
①当点![]() 运动到
运动到![]() 时,线段
时,线段![]() 长为
长为![]() .
.
②点![]() 沿直线从
沿直线从![]() 运动到
运动到![]() .
.
③点![]() 沿圆弧从
沿圆弧从![]() 运动到
运动到![]() .
.
(![]() )点
)点![]() 从点
从点![]() 运动至
运动至![]() 的过程中,点
的过程中,点![]() 到
到![]() 的距离的最小值是__________.
的距离的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们,如果每人送3本,则剩余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,设该校买了m本课外读物,有![]() x名学生获奖,请解答下列问题:
x名学生获奖,请解答下列问题:
(1)用含x的代数式表示m;
(2)求出该校的获奖人数及所买课外读物的本数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com