
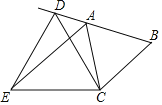
【题目】如图,等边△ABC的边长为4,D是线段BA延长线上的一点,以线段CD为边向CD的左侧作等边△CDE,连接AE.
(1)△ABC的面积S△ABC= ;
(2)求证:△ACE≌△BCD;
(3)若四边形ABCE的面积为10![]() ,求AD的长.
,求AD的长.
【答案】(1)4![]() ;(2)见解析;(3)AD=2.
;(2)见解析;(3)AD=2.
【解析】
(1)作高线,根据等边三角形的性质计算高的长,根据三角形面积公式可得结论;
(2)根据SAS证明三角形全等;
(3)根据等量代换可得:S△ACE+S△ACB=S△BCD+S△ACB=10![]() ,由(1)可计算△BCD的面积,从而计算BD的长,可得结论.
,由(1)可计算△BCD的面积,从而计算BD的长,可得结论.
解:(1)如图,过C作CF⊥AB于F,
∵△ABC是等边三角形,且AB=BC=AC=4,
∴∠FCB=30°,
∴BF=2,CF=2![]() ,
,
∴S△ABC=![]() =
=![]() =4
=4![]() ;
;
故答案为:4![]() ;
;
(2)∵△CDE是等边三角形,
∴CE=CD,∠ECD=60°,
∴∠ECD=∠ACB=60°,
∴∠ACE=∠BCD,
∵AC=BC,
∴△ACE≌△BCD(SAS);
(3)∵四边形ABCE的面积为10![]() ,
,
∴S△ACE+S△ACB=S△BCD+S△ACB=10![]() ,
,
∵S△ABC=![]() =
=![]() =4
=4![]() ,
,
∴S△BCD=6![]() ,
,
∴![]() =6
=6![]() ,即
,即![]() BD
BD![]() =6
=6![]() ,
,
∴BD=6,
∵AB=4,
∴AD=2.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件不能判定Rt△ABC≌Rt△DEF的是( )
A. AC=DF,∠B=∠EB. ∠A=∠D,∠B=∠E
C. AB=DE,AC=DFD. AB=DE,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设,首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④),这样反复更换地砖的颜色,按照这种规律,直至铺满整个广场,观察下图,解决下列问题.
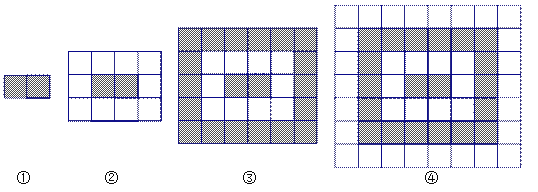
(1)填表
图形序号数 | ① | ② | ③ | ④ | … |
地砖总数(包括黑白地砖) | 2 |
(2)按照这种规律第6个图形一共用去地砖多少块?
(3)按照这种规律第![]() 个图形一共用去地砖多少块?(用含
个图形一共用去地砖多少块?(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 中
中![]() 与
与![]() 交于
交于![]() 点,点
点,点![]() 在线段
在线段![]() 上,作直线
上,作直线![]() 交直线
交直线![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,设直线
,设直线![]() 交
交![]() 于
于![]() .
.

(1)如图,当![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() ;
;
(2)如图2,当![]() 在线段
在线段![]() 上,连接
上,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(3)在图3,当![]() 在线段
在线段![]() 上,连接
上,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
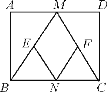
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB与AD满足什么条件时,四边形MENF是正方形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com