
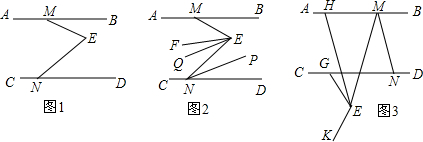
分析 (1)过点E作l∥AB,利用平行线的性质可得∠1=∠BME,∠2=∠DNE,由∠MEN=∠1+∠2,等量代换可得结论;
(2)利用角平分线的性质可得$∠NEF=\frac{1}{2}∠MEN,∠ENP=\frac{1}{2}∠END$,由EQ∥NP,可得$∠QEN=∠ENP=\frac{1}{2}∠END$,由(1)的结论可得∠MEN=∠BME+∠END,等量代换得出结论;
(3)由已知可得$∠EMN=\frac{1}{n}∠BMN$,$∠GEM=\frac{1}{n}∠GEK$,由EH∥MN,可得$∠HEM=∠ENM=\frac{1}{n}∠BMN$,因为∠GEH=∠GEM-∠HEM,等量代换得出结论.
解答 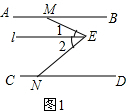 解:(1)如图1,过点E作l∥AB,
解:(1)如图1,过点E作l∥AB,
∵AB∥CD,
∴l∥AB∥CD,
∴∠1=∠BME,∠2=∠DNE,
∵∠MEN=∠1+∠2,
∴∠E=∠BME+∠END,
故答案为:∠E=∠BME+∠END;
(2)如图2,∵EF平分∠MEN,NP平分∠END,
∴$∠NEF=\frac{1}{2}∠MEN,∠ENP=\frac{1}{2}∠END$,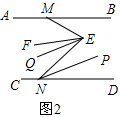
∵EQ∥NP,
∴$∠QEN=∠ENP=\frac{1}{2}∠END$,
∵∠MEN=∠BME+∠END,
∴∠MEN-∠END=∠BME=m°,
∴∠FEQ=∠NEF-∠NEQ
=$\frac{1}{2}∠MEN-\frac{1}{2}∠END$,
=$\frac{1}{2}(∠MEN-∠END)$
=$\frac{1}{2}$m°;
(3)n∠GEH=∠GEK-∠BMN.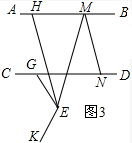
如图3,∵∠BMN=n•∠EMN,∠GEK=n•∠GEM,
∴$∠EMN=\frac{1}{n}∠BMN$,$∠GEM=\frac{1}{n}∠GEK$,
∵EH∥MN,
∴$∠HEM=∠ENM=\frac{1}{n}∠BMN$,
∵∠GEH=∠GEM-∠HEM,
=$\frac{1}{n}∠GEK-\frac{1}{n}∠BMN$,
∴n∠GEH=∠GEK-∠BMN.
点评 本题主要考查了平行线的性质,作出适当的辅助线,结合图形等量代换是解答此题的关键.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com