
分析 ①两边直接开平方即可;
②把常数项-4移项后,应该在左右两边同时加上一次项系数3的一半的平方;
③分解因式后得到(x-4)(x+2)=0,推出方程x-4=0,x+2=0,求出方程的解即可;
④提取公因式(x+2)后,再解两个一元一次方程即可.
解答 解:①∵(2x-1)2=9,
∴2x-1=±3,
∴2x=4或2x=-2,
∴x1=4,x2=-1;
②∵x2+3x-4=0,
∴(x+4)(x-1)=0,
∴x+4=0或x-1=0,
∴x1=-4,x2=1;
③∵x2-2x-8=0,
∴(x+2)(x-4)=0,
∴x+2=0或x-4=0,
∴x1=-2,x2=4;
④∵(x+1)(x+2)=2x+4,
∴(x+2)(x+1-2)=0,
∴x+2=0或x-1=0,
∴x1=-2,x2=1.
点评 本题主要考查了解一元二次方程的知识,根据方程的特点选择合适的方法解一元二次方程是解决此类问题的关键.一般解一元二次方程的方法有直接开平方法、因式分解法、公式法、配方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-2=(x+3)2 | B. | x2-1=0 | C. | x2+$\frac{3}{x}$-5=0 | D. | ax2+bx+c=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
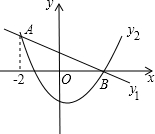 直线y1=kx+m与抛物线y2=ax2+bx+c在同一坐标中的图象如图所示,直线与抛物线相交于A(-2,2)、B(3,0),当x取值范围是-2<x<3时,y1>y2.
直线y1=kx+m与抛物线y2=ax2+bx+c在同一坐标中的图象如图所示,直线与抛物线相交于A(-2,2)、B(3,0),当x取值范围是-2<x<3时,y1>y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com