
【题目】在平面直角坐标系中,点0为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于点B,C,与y轴交于点A,点A的坐标为(0,![]() ),点D为抛物线的顶点.
),点D为抛物线的顶点.
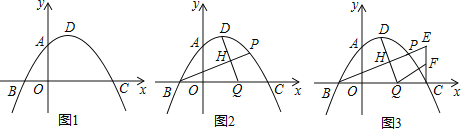
(1)如图1,求拋物线的顶点D的坐标;
(2)如图2,点P是第一象限内对称轴右侧拋物线上一点,连接PB,过点D作DQ⊥BP于点H,交x轴于点Q,设点P的横坐标为m,点Q的横坐标为n,求n与m的函数关系式;
(3)如图3,在(2)的条件下,过点C作CE∥y轴交BP的延长线于点E,点F为CE的中点,连接FQ,若∠DQC+∠CQF=135°,求点P的坐标.
【答案】(1)D(1,2);(2)n=4﹣m;(3)P(![]() ,
,![]() ).
).
【解析】
(1)将点A代入抛物线解析式可求出a,抛物线解析式和顶点D可求.
(2)分别过点D、P作x轴的垂线,可得到三角形相似,用点坐标转换线段长度,列比例关系就可以得到m和n的函数关系.
(3)用点坐标转换为线段长度,可以得到相关线段的长度相等,从而得到全等三角形及相似三角形,列比例关系就可以得到点P的坐标.
(1)将点A(0,![]() )代入抛物线中,
)代入抛物线中,
﹣3a=![]() ,
,
解得a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+x+
x2+x+![]() ,
,
∵﹣![]() =1,解得y=2,
=1,解得y=2,
∴D(1,2).
(2)如图1所示,过点D作DH垂直于x轴于点H,过点P作PN垂直于x轴于点N,
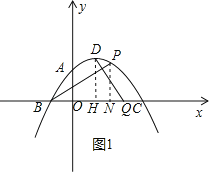
∴DH=2,QH=n﹣1,PN=![]() ,BN=m+1,
,BN=m+1,
∵△BPN∽△DHQ,
∴![]() ,即
,即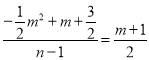 ,
,
解得n=4﹣m.
(3)如图2所示,
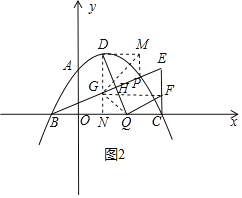
∵D(1,2),Q(4﹣m,0),C(3,0)B(﹣1,0),
∴BN=2,DN=2,NQ=3﹣m,
∵∠BNG=∠DNQ,∠NDQ=∠GBN,
∴△BGN≌△DNQ(ASA),
∴GN=NQ=3﹣m,
连接GQ,
∴∠GQN=45°,
∵∠DQC+∠FQC=135°,
∴∠GQD=∠FQC,
∵DG=m﹣1,
过点P作y轴的平行线PM,过点D作x轴的平行线交MP于点M,连接MG,
∴MD=m﹣1,
∴MD=DG,
∴∠DGM=45°,
∵∠NGQ=45°,
∴∠MGQ=90°,
∴∠MGP=∠GQD=∠FQC,
连接GF,GF∥BC,
∴∠GFQ=∠FQC=∠MGP,∠FGQ=∠GMP=45°,
∴△GMP∽△GQF,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]()
∴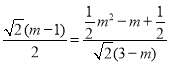 ,
,
解得m1=1(舍),m2=![]() ,
,
∴m=![]() ,
,
∴P(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如下表:

(1)过程表中数据,分别直接写出m与x,n与x的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
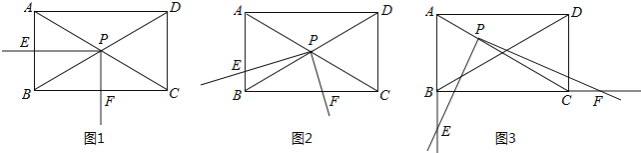
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家,爱园艺”、
.“爱我家,爱园艺”、![]() .“园艺小清新之旅”和
.“园艺小清新之旅”和![]() .“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
.“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李欣选择线路![]() .“园艺小清新之旅”的概率是多少?
.“园艺小清新之旅”的概率是多少?
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一线路游览的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格纸中,每一个小正方形的边长为一线段AB的两个端点都在小正方形的顶点上,请按下面的要求画图.
(1)在图1中画钝角三角形ABC,点C落在小正方形顶点上,其中△ABC有一个内角为135°,△ABC的面积为4,并直接写出∠ABC的正切值;
(2)在图1中沿小正方形网格线画一条裁剪线,沿此裁剪线将钝角三角形ABC分隔成两部分图形,按所裁剪图形的实际大小,将这两部分图形在图2中拼成一个平行四边形DEFG,要求裁成的两部分图形在拼成平行四边形时互不重叠且不留空隙,其中所拼成的平行四边形的周长为8+2![]() ,各顶点必须与小正方形的顶点重合.
,各顶点必须与小正方形的顶点重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
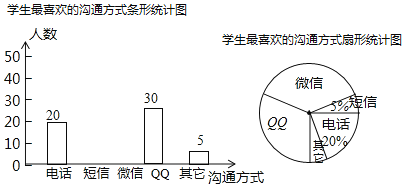
(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
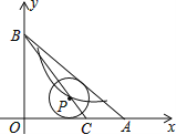
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,单价30元,试销中发现这种商品每天的销售量夕(件)与每件的销售价![]() (元)满足关系:
(元)满足关系:![]() =100-2
=100-2![]() .若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
.若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
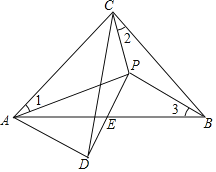
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,在△ABC内一点P,已知∠1=∠2=∠3,将△BCP以直线PC为对称轴翻折,使点B与点D重合,PD与AB交于点E,连结AD,将△APD的面积记为S1,将△BPE的面积记为S2,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com