
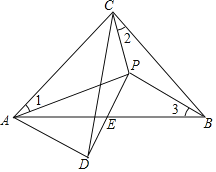
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,在△ABC内一点P,已知∠1=∠2=∠3,将△BCP以直线PC为对称轴翻折,使点B与点D重合,PD与AB交于点E,连结AD,将△APD的面积记为S1,将△BPE的面积记为S2,则![]() 的值为_____.
的值为_____.
【答案】![]()
【解析】
首先证明∠APC=90°,∠BPC=∠APB=∠ADB=135°,再证明△PDB,△ADP都是等腰直角三角形即可解决问题.
如图,连接BD.
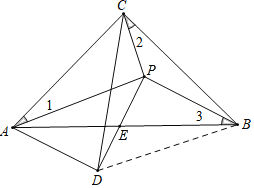
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠1=∠2,∠2+∠ACP=90°,
∴∠1+∠ACP=90°,
∴∠APC=90°,
∵∠2=∠3,∠3+∠PBC=45°,
∴∠2+∠PBC=45°,
∴∠BPC=∠DPC=135°,
∴∠APD=45°,∠DPB=90°,
∵PD=PB,
∴△PDB是等腰直角三角形,
同法可知:∠APB=135°,
∴∠APD=45°,
∵CA=CD=CB,
∴∠CAD=∠CDA,∠CDB=∠CBD,
∵∠ACD+2∠CDA=180°,∠DCB+2∠CDB=180°,∠ACD+∠DCB=90°,
∴2∠ADC+2∠CDB=270°,
∴∠ADP=∠ADC+∠CDB=135°,
∵∠PDB=45°,
∴∠ADP=90°,
∵∠APD=45°,
∴△APD是等腰直角三角形,
∴AD=PD=PB,
∵∠ADP=∠DPB=90°,
∴AD∥PB,
∴四边形ADBP是平行四边形,
∴PE=DE,
∴S2=![]() S△DPB
S△DPB![]() S△ADP=
S△ADP=![]() S1.
S1.
∴![]() =
=![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点0为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于点B,C,与y轴交于点A,点A的坐标为(0,![]() ),点D为抛物线的顶点.
),点D为抛物线的顶点.
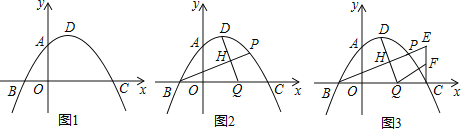
(1)如图1,求拋物线的顶点D的坐标;
(2)如图2,点P是第一象限内对称轴右侧拋物线上一点,连接PB,过点D作DQ⊥BP于点H,交x轴于点Q,设点P的横坐标为m,点Q的横坐标为n,求n与m的函数关系式;
(3)如图3,在(2)的条件下,过点C作CE∥y轴交BP的延长线于点E,点F为CE的中点,连接FQ,若∠DQC+∠CQF=135°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
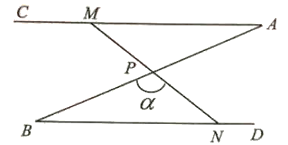
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生每天参加体育锻炼额时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):
30 60 70 10 30 115 70 60 75 90 15 70 40 75 105 80 60 30 70 45
对以上数据进行整理分析,得到下列表一和表二:
表一
时间t(单位:分钟) |
|
|
|
|
人数 | 2 | a | 10 | b |
表二
平均数 | 中位数 | 众数 |
60 | c | d |
根据以上提供信息,解答下列问题:
(1)填空
①a= b=
②c= d=
(2)如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
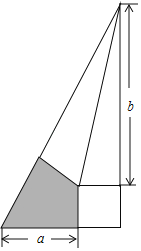
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将抛物线P1:y1=![]() x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
(1)当m=1时,a= ,h= ,k= ;
(2)在(1)的条件下,当y1<y2<0时,求x的取值范围;
(3)如图2,过点C1作y轴的垂线,分别交抛物线P1,P2于D、E两点,当四边形A1DEB是矩形时,求m的值.
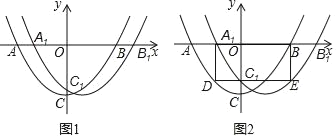
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直线![]() 与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
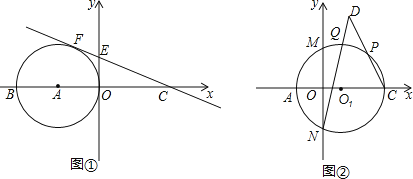
(1)求![]() 的半径;
的半径;
(2)连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.
(3)如图②,以AC为直径作![]() 交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() 为
为![]() 内一点,将
内一点,将![]() 绕点
绕点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() 得到
得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,且
,且![]() 三点在同一直线上.
三点在同一直线上.
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)如图2,若![]() ,请补全图形,再过点
,请补全图形,再过点![]() 作
作![]() 于点
于点![]() ,然后探究线段
,然后探究线段![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)若![]() ,且点
,且点![]() 满足
满足![]() ,直接写出点
,直接写出点![]() 到
到![]() 的距离.
的距离.
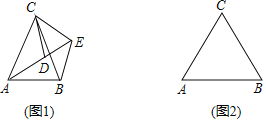
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com