
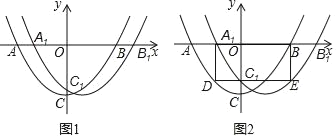
【题目】如图1,将抛物线P1:y1=![]() x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
(1)当m=1时,a= ,h= ,k= ;
(2)在(1)的条件下,当y1<y2<0时,求x的取值范围;
(3)如图2,过点C1作y轴的垂线,分别交抛物线P1,P2于D、E两点,当四边形A1DEB是矩形时,求m的值.
【答案】(1)![]() ;﹣1,﹣3(2)﹣2<x<
;﹣1,﹣3(2)﹣2<x<![]() (3)
(3)![]()
【解析】
(1)根据平移的坐标特征写出抛物线平移后得到的解析式,与抛物线P2解析式对应即得到a、h、k的值.
(2)把y1<y2<0拆分成两部分:①求y2<0时x的取值范围,先求出抛物线P2与x轴两交点坐标,由图象可知在抛物线中间部分在x轴下方,即对应的x范围;②求y1<y2时x的取值范围,先由两二次函数值相等求得两抛物线交点横坐标,根据图象找出x对应的取值范围;①②部分要同时成立,即求关于x的两个不等式组的公共解.
(3)根据平移后图象上所有点平移的距离相等,都是m,得到AA1=DC1=m,由四边形A1DEB是矩形易证四边形A1DC1O是矩形,即得到OA=AA1+OA1=2m=3.
解:(1)∵抛物线P1:y1=![]() x2﹣3右移m个单位长度得到新抛物线解析式为:y2=
x2﹣3右移m个单位长度得到新抛物线解析式为:y2=![]() (x﹣m)2﹣3
(x﹣m)2﹣3
∴y2=a(x+h)2+k=![]() (x﹣m)2﹣3
(x﹣m)2﹣3
又∵m=1
∴h=﹣m=﹣1
故答案为:![]() ;﹣1,﹣3
;﹣1,﹣3
(2)∵当y2=![]() (x﹣1)2﹣3=0时,
(x﹣1)2﹣3=0时,
解得:x1=﹣2,x2=4
∴由图象可知,当﹣2<x<4时,y2<0
当y1=y2时,![]() x2﹣3=
x2﹣3=![]() (x﹣1)2﹣3
(x﹣1)2﹣3
解得:x=![]() ,
,
∴由图象可知,当x<![]() 时,y1<y2
时,y1<y2
∴当y1<y2<0时,x的取值范围是﹣2<x<![]()
(3)当y1=![]() x2﹣3=0时,解得:x=±3
x2﹣3=0时,解得:x=±3
∴A(﹣3,0),OA=3
根据平移性质得:AA1=DC1=m
∵四边形A1DEB是矩形
∴∠A1DE=∠DA1B=90°
∴四边形A1DC1O是矩形
∴OA1=DC1=m
∴OA=AA1+OA1=2m=3
∴m=![]()


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
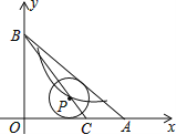
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+2的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
(1)请求出二次函数的解析式;
(2)若点M(m,n)在抛物线的对称轴上,且AM平分∠OAC,求n的值.
(3)若P是线段AB上的一个动点(不与A、B重合),过P作PQ∥AC,与AB上方的抛物线交于点Q,与x轴交于点H,试问:是否存在这样的点Q,使PH=2QH?若存在,请直接出点Q的坐标;若不存在,请说明理由.
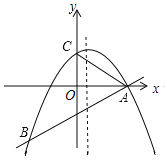
查看答案和解析>>
科目:初中数学 来源: 题型:
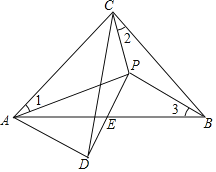
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,在△ABC内一点P,已知∠1=∠2=∠3,将△BCP以直线PC为对称轴翻折,使点B与点D重合,PD与AB交于点E,连结AD,将△APD的面积记为S1,将△BPE的面积记为S2,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元;
(1)求键盘和鼠标的单价各是多少元?
(2)经过与经销商洽谈,键盘打八折,鼠标打八五折.若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
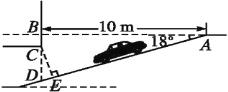
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1,则圆的半径r的取值范围是 ( )
A.r>4 B.0<r<6 C.4≤r<6 D.4<r<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.

(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形ADBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
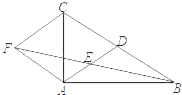
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,连接BE,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)在不添加任何辅助线的情况下,请直接写出图中四个三角形,使写出的每个三角形的面积等于△AEF面积的2倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com