
【题目】如图所示,二次函数y=ax2+bx+2的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
(1)请求出二次函数的解析式;
(2)若点M(m,n)在抛物线的对称轴上,且AM平分∠OAC,求n的值.
(3)若P是线段AB上的一个动点(不与A、B重合),过P作PQ∥AC,与AB上方的抛物线交于点Q,与x轴交于点H,试问:是否存在这样的点Q,使PH=2QH?若存在,请直接出点Q的坐标;若不存在,请说明理由.
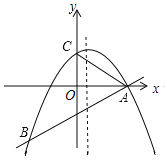
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)2
x+2;(2)2![]() ﹣6;(3)存在,点Q(﹣
﹣6;(3)存在,点Q(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)将点A、B的坐标代入函数表达式,即可求解;
(2)如图,过点A作∠A的角平分线交y轴于点M,则由勾股定理得:(2﹣x)2=x2+(2![]() ﹣4)2,解得:x=4
﹣4)2,解得:x=4![]() ﹣8,即可求解;
﹣8,即可求解;
(3)确定直线AB、直线PQ的表达式,联立求得点Q(2﹣2![]() ,﹣1﹣c+
,﹣1﹣c+![]() ),由PH=2QH,则P、Q的纵坐标之比也为2,即可求解.
),由PH=2QH,则P、Q的纵坐标之比也为2,即可求解.
解:(1)将点A、B的坐标代入函数表达式得:![]() ,解得:
,解得: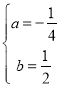 ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)如图,过点A作∠A的角平分线交y轴于点M,交二次函数对称轴于点G,
过点M作MN⊥AC于点N,二次函数对称轴交AM、x轴于点G、H,
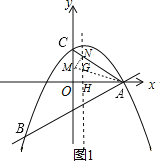
设:OM=x=MN,则AM=OA=4,
AC=2![]() ,OC=2,CM=2﹣x,CN=CA﹣AN=2
,OC=2,CM=2﹣x,CN=CA﹣AN=2![]() ﹣4,
﹣4,
则由勾股定理得:(2﹣x)2=x2+(2![]() ﹣4)2,解得:x=4
﹣4)2,解得:x=4![]() ﹣8,
﹣8,
∴GH∥OM,则![]() ,即:
,即:![]() ,
,
则n=GH=![]() x=2
x=2![]() ﹣6;
﹣6;
(3)存在,理由:
如图:
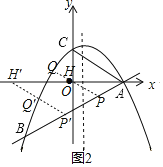
将点B、A的坐标代入一次函数表达式并解得:
直线AB的表达式为:y=![]() x﹣2①,
x﹣2①,
同理直线AC的表达式为:y=﹣![]() x+2,
x+2,
∵PQ∥AC,则设直线PQ的表达式为:y=﹣![]() x﹣c(c>0)②,
x﹣c(c>0)②,
联立①②并解得:x=2±2![]() (舍去正值),
(舍去正值),
故点Q(2﹣2![]() ,﹣1﹣c+
,﹣1﹣c+![]() ),
),
∵PH=2QH,
∴P、Q的纵坐标之比也为2,
即﹣![]() c﹣1=±2(﹣1﹣c+
c﹣1=±2(﹣1﹣c+![]() ),
),
解得:c=![]() 或
或![]() ,
,
故点Q(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
查看答案和解析>>
科目:初中数学 来源: 题型:
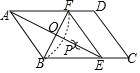
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径两弧交AD于点F,再分别以点B,F为圆心,大于![]() BF为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)AB AF(选填“=”,“≠”,“>”,“<”):AE ∠BAD的平分线.(选填“是”或“不是”)
(2)在(1)的条件下,求证:四边形ABEF是菱形.
(3)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
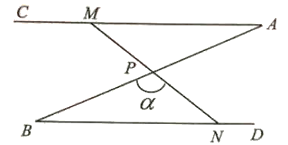
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018年梧州市体育中考中,每名学生需考3个项目(包括2个必考项目与1个选考项目)每个项目20分,总分60分.其中必考项目为:跳绳和实心球;选考项目:A篮球、B足球、C排球、D立定跳远、E50米跑,F女生800米跑或男生1000米跑.某兴趣小组随机对同学们的选考项目做了调查,根据调查结果绘制了两幅不完整的条形统计图与扇形统计图.结合图中信息,回答下列问题:
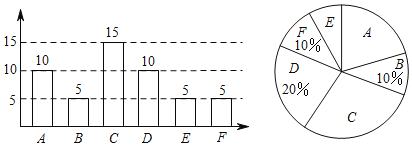
(1)在这次调查中,一共调查了 名学生,扇形统计图中C对应的圆心角的度数为 ;
(2)在本次调查的必考项目的众数是 ;(填A、B、C、D、E、F选项)
(3)选考项目包括球类与非球类,请用树状图或列表法求甲、乙两名同学都选球类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生每天参加体育锻炼额时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):
30 60 70 10 30 115 70 60 75 90 15 70 40 75 105 80 60 30 70 45
对以上数据进行整理分析,得到下列表一和表二:
表一
时间t(单位:分钟) |
|
|
|
|
人数 | 2 | a | 10 | b |
表二
平均数 | 中位数 | 众数 |
60 | c | d |
根据以上提供信息,解答下列问题:
(1)填空
①a= b=
②c= d=
(2)如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
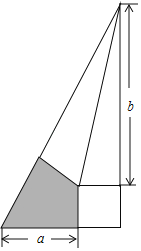
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
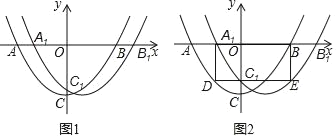
【题目】如图1,将抛物线P1:y1=![]() x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
(1)当m=1时,a= ,h= ,k= ;
(2)在(1)的条件下,当y1<y2<0时,求x的取值范围;
(3)如图2,过点C1作y轴的垂线,分别交抛物线P1,P2于D、E两点,当四边形A1DEB是矩形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B,
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O 的半径.
,求⊙O 的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com