
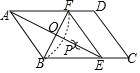
����Ŀ����ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() BFΪ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
BFΪ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��1��AB�� ��AF��ѡ�������������١���������������������AE�� ����BAD��ƽ���ߣ���ѡ��������������������
��2���ڣ�1���������£���֤���ı���ABEF�����Σ�
��3��AE��BF�ཻ�ڵ�O�����ı���ABEF���ܳ�Ϊ40��BF��10����AE�ij�Ϊ�� ������ABC���� ������
���𰸡���1�������ǣ���2������������3��![]() .
.
��������
��1�����ݽ�ƽ�ֵ����ʺͳ߹���ͼԭ�����ɵõ��𰸣�
��2����֤����AEB�ա�AEF���Ƴ���EAB=��EAF����AD��BC���Ƴ���EAF=��AEB=��EAB���õ�BE=AB=AF���ɴ˼���֤����
��3���������ε���������֤����AOB�Ǻ���30����ֱ�������Σ��ɴ˼��ɽ�����⣮
��1���⣺AB��AF��AEƽ�֡�BAD��ƽ���ߣ�
�ʴ�Ϊ�����ǣ�
��2��֤������AEƽ�֡�BAF��
���BAE����FAE��
��AF��BE��
���BAE����BEA��
��AB��EB��
��AF��AB��
��AF��BE��AF��BE��
���ı���ABEFΪƽ���ı��Σ�
��AB��AF��
���ı���ABEF�����Σ�
��3���⣺���ı���ABEF�����Σ�
���ı���ABEF���ܳ�Ϊ40��
��AB��10��OA��OE��OB��OF��5��AE��BF��
���ABFΪ�ȱ������Σ�
���BAF��60����
���ABC��120����
��OA��![]() OB��5
OB��5![]() ��
��
��AE��2OA��10![]() ��
��
�ʴ�Ϊ10![]() ��120��
��120��



 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�����о�С�����������ס����������������������һ���������̽������������:
�������:
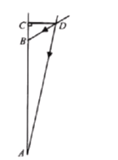
����ͼ��ijס�������Ϸ���װ�������Ҫ����Ƶ��������������ȵ��ڵ��������ȵ����⣬��������ȵ�ʹ������ů��������������.

�������:
����ͼ������ѧ�����о�С��ͨ�������о�����˴�ֱ��ǽ��![]() ��������
��������![]()
�����ռ�:
ͨ������������Ϻ�ʵ�ʲ�����������һ���У�������һ�������ʱ�̣�̫������![]() ��������
��������![]() �ļн�
�ļн�![]() ���
���![]() ����������һ�������ʱ�̣�̫������
����������һ�������ʱ�̣�̫������![]() ��������
��������![]() �ļн�
�ļн�![]() ��С��
��С��![]() ���������ĸ߶�
���������ĸ߶�![]()
������:
�����������������ݣ���������![]() �ij�.(�����ȷ��
�ij�.(�����ȷ��![]() ,�ο����ݣ�
,�ο����ݣ�![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������ֽ�У�ÿһ��С�����εı߳�Ϊһ�߶�AB�������˵㶼��С�����εĶ����ϣ��밴�����Ҫ��ͼ��
(1)��ͼ1�л��۽�������ABC����C����С�����ζ����ϣ����С�ABC��һ���ڽ�Ϊ135�㣬��ABC�����Ϊ4����ֱ��д����ABC������ֵ��
(2)��ͼ1����С������������һ���ü��ߣ��ش˲ü��߽��۽�������ABC�ָ���������ͼ�Σ������ü�ͼ�ε�ʵ�ʴ�С������������ͼ����ͼ2��ƴ��һ��ƽ���ı���DEFG��Ҫ��óɵ�������ͼ����ƴ��ƽ���ı���ʱ�����ص��Ҳ�����϶��������ƴ�ɵ�ƽ���ı��ε��ܳ�Ϊ8+2![]() �������������С�����εĶ����غϣ�
�������������С�����εĶ����غϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
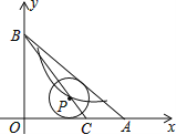
����Ŀ����ͼ����Rt��OAB�У�OA=4��AB=5����C��OA�ϣ�AC=1����P��Բ��P���߶�BC�ϣ��ҡ�P���AB��AO�����У�������������![]() ��k��0����ͼ��Բ��P����k=________________��
��k��0����ͼ��Բ��P����k=________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+cͼ���һ���֣��������ߵĶԳ���Ϊx����1����ô����˵����ȷ���ǣ�������
��b2��4ac����abc��0����2a+b��0����a+b+c��0����a��b+c��0��

A. �٢ڢۢ�B. �ڢܢ�C. �ڢۢ�D. �٢ܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ����Ʒ������30Ԫ�������з���������Ʒÿ���������Ϧ��������ÿ�������ۼ�![]() ��Ԫ�������ϵ��
��Ԫ�������ϵ��![]() =100-2
=100-2![]() �����̵�ÿ������������ƷҪ���200Ԫ������������ôÿ����Ʒ���ۼ�Ӧ��Ϊ����Ԫ?ÿ��Ҫ�۳�������Ʒ���ټ�?
�����̵�ÿ������������ƷҪ���200Ԫ������������ôÿ����Ʒ���ۼ�Ӧ��Ϊ����Ԫ?ÿ��Ҫ�۳�������Ʒ���ټ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
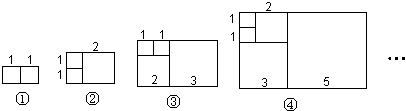
����Ŀ�������������ѧ��쳲��������о����ӷ�ֳ����ʱ������������һ������1��1��2��3��5��8��13���������дӵ���������ÿһ������������ǰ���������ĺ��������������еĸ�������Ϊ�����εı߳�ֵ���������Σ��ٷֱ����δ�����ȡ2����3����4����5����������ƴ�����ϳ����Σ������˹��ɼ����������Σ������Ϊ���ij������ܳ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����κ���y��ax2+bx+2��ͼ����A��4��0����B����4����4��������y�ύ�ڵ�C��
��1����������κ����Ľ���ʽ��
��2������M��m��n���������ߵĶԳ����ϣ���AMƽ�֡�OAC����n��ֵ��
��3����P���߶�AB�ϵ�һ�����㣨����A��B�غϣ�����P��PQ��AC����AB�Ϸ��������߽��ڵ�Q����x�ύ�ڵ�H�����ʣ��Ƿ���������ĵ�Q��ʹPH��2QH�������ڣ���ֱ�ӳ���Q�����ꣻ�������ڣ���˵�����ɣ�
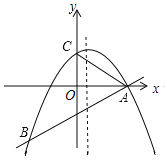
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��Ե�(3����5)ΪԲ�ģ�rΪ�뾶��Բ�����ҽ������㵽x������ֱ�ߵľ������1����Բ�İ뾶r��ȡֵ��Χ�� ( )
A��r>4 B��0<r<6 C��4��r<6 D��4<r<6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com