
【题目】如图,在正方形网格纸中,每一个小正方形的边长为一线段AB的两个端点都在小正方形的顶点上,请按下面的要求画图.
(1)在图1中画钝角三角形ABC,点C落在小正方形顶点上,其中△ABC有一个内角为135°,△ABC的面积为4,并直接写出∠ABC的正切值;
(2)在图1中沿小正方形网格线画一条裁剪线,沿此裁剪线将钝角三角形ABC分隔成两部分图形,按所裁剪图形的实际大小,将这两部分图形在图2中拼成一个平行四边形DEFG,要求裁成的两部分图形在拼成平行四边形时互不重叠且不留空隙,其中所拼成的平行四边形的周长为8+2![]() ,各顶点必须与小正方形的顶点重合.
,各顶点必须与小正方形的顶点重合.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:

①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
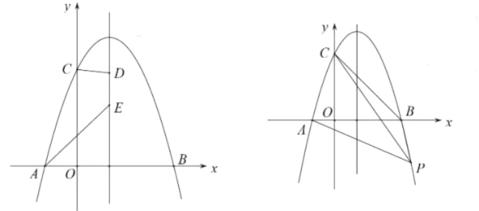
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
查看答案和解析>>
科目:初中数学 来源: 题型:
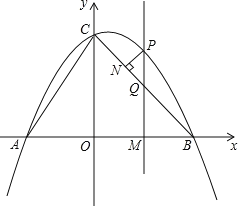
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .点
.点![]() 是第一象限内抛物线上的一个动点,点
是第一象限内抛物线上的一个动点,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求此抛物线的表达式;
(2)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() .试探究点P在运动过程中,是否存在这样的点
.试探究点P在运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形.若存在,请求出此时点
为顶点的三角形是等腰三角形.若存在,请求出此时点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .请用含
.请用含![]() 的代数式表示线段
的代数式表示线段![]() 的长,并求出当
的长,并求出当![]() 为何值时
为何值时![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
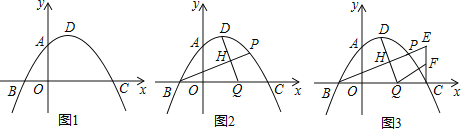
【题目】在平面直角坐标系中,点0为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于点B,C,与y轴交于点A,点A的坐标为(0,![]() ),点D为抛物线的顶点.
),点D为抛物线的顶点.
(1)如图1,求拋物线的顶点D的坐标;
(2)如图2,点P是第一象限内对称轴右侧拋物线上一点,连接PB,过点D作DQ⊥BP于点H,交x轴于点Q,设点P的横坐标为m,点Q的横坐标为n,求n与m的函数关系式;
(3)如图3,在(2)的条件下,过点C作CE∥y轴交BP的延长线于点E,点F为CE的中点,连接FQ,若∠DQC+∠CQF=135°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
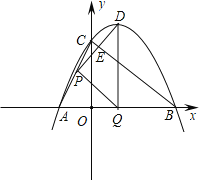
【题目】如图,抛物线y=ax2+bx+3![]() 与x轴交于A(﹣3,0),B(9,0)两点,与y轴交于点C,连接AC,BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,连接PD与BC交于点E.设点P的运动时间为t秒(t>0)
与x轴交于A(﹣3,0),B(9,0)两点,与y轴交于点C,连接AC,BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,连接PD与BC交于点E.设点P的运动时间为t秒(t>0)
(1)求抛物线的表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简).
②在点P,Q运动的过程中,当PQ=PD时,求t的值;
(3)点M为线段BC上一点,在点P,Q运动的过程中,当点E为PD中点时,是否存在点M使得PM+![]() BM的值最小?若存在,请求出PM+
BM的值最小?若存在,请求出PM+![]() BM的最小值;若不存在,请说明理由.
BM的最小值;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
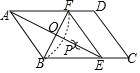
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径两弧交AD于点F,再分别以点B,F为圆心,大于![]() BF为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)AB AF(选填“=”,“≠”,“>”,“<”):AE ∠BAD的平分线.(选填“是”或“不是”)
(2)在(1)的条件下,求证:四边形ABEF是菱形.
(3)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
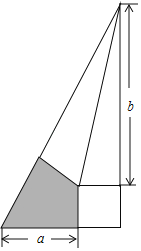
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com