
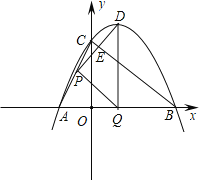
【题目】如图,抛物线y=ax2+bx+3![]() 与x轴交于A(﹣3,0),B(9,0)两点,与y轴交于点C,连接AC,BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,连接PD与BC交于点E.设点P的运动时间为t秒(t>0)
与x轴交于A(﹣3,0),B(9,0)两点,与y轴交于点C,连接AC,BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,连接PD与BC交于点E.设点P的运动时间为t秒(t>0)
(1)求抛物线的表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简).
②在点P,Q运动的过程中,当PQ=PD时,求t的值;
(3)点M为线段BC上一点,在点P,Q运动的过程中,当点E为PD中点时,是否存在点M使得PM+![]() BM的值最小?若存在,请求出PM+
BM的值最小?若存在,请求出PM+![]() BM的最小值;若不存在,请说明理由.
BM的最小值;若不存在,请说明理由.
![]()
【答案】(1)![]() ;(2)P
;(2)P  ,D
,D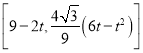 ;
;
![]() ;(3)存在,故PM+
;(3)存在,故PM+![]() BM的最小值为
BM的最小值为![]() .
.
【解析】
(1)把A(﹣3,0),B(9,0)两点,代入解析式即可
(2)先求出BC的解析式①把P,Q代入解析式即可解答
②当PQ=PD时,则DQ中点的纵坐标=点P的纵坐标,在代入解析式即可
(3)根据点E是PQ的中点,求出点E的坐标,将其代入解析式②即可求出P,作点P关于直线BC的对称点P′,过点P′作P′H⊥x轴、BC于点H、M,过点P作PN⊥y轴于点N,再证明△P′MC≌△PNC(AAS),即可解答
解:(1)将A(﹣3,0),B(9,0)代入y=ax2+bx+3![]() ,得:
,得:
![]() ,解得:
,解得: ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+3
x+3![]() ①;
①;
(2)由题意得:∠ACO=∠OBC=30°,∠ACB=90°,
将点B、C(0,3![]() )的坐标代入一次函数表达式并解得:
)的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣![]() x+3
x+3![]() ②;
②;
①点P的坐标为(﹣3+![]() t,
t,![]() t),
t),
点Q(9﹣2t,0),将点Q的坐标代入①式并整理得:点D[9﹣2t,![]() (6t﹣t2)];
(6t﹣t2)];
②当PQ=PD时,则DQ中点的纵坐标=点P的纵坐标,
即:![]() [
[![]() (6t﹣t2)]=
(6t﹣t2)]=![]() t,
t,
解得:t=![]() ;
;
(3)点P的坐标为(﹣3+![]() t,
t,![]() t)、点D[9﹣2t,
t)、点D[9﹣2t,![]() (6t﹣t2)],
(6t﹣t2)],
点E是PQ的中点,则点E[3﹣![]() t,
t,![]() t+
t+![]() (6t﹣t2)],
(6t﹣t2)],
将点E的坐标代入②式并整理得:t2﹣6t+9=0,解得:t=3,
即点P(﹣![]() ,
,![]() )即点P是AC的中点,
)即点P是AC的中点,
作点P关于直线BC的对称点P′,过点P′作P′H⊥x轴、BC于点H、M,过点P作PN⊥y轴于点N,
则MH=![]() MB,
MB,
则此时,PM+![]() BM=PM+MH=P′H为最小值,
BM=PM+MH=P′H为最小值,
∵∠ACB=90°,PC=P′C,∠P′CM=∠NCP,∠P′MC=∠PNC=90°,
∴△P′MC≌△PNC(AAS),∴MC=NC=![]() OC,
OC,
OM=![]() OC=
OC=![]() =P′H,
=P′H,
故PM+![]() BM的最小值为
BM的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频数分布直方图(数据分成7组:
30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
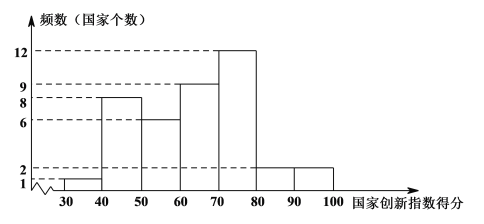
b.国家创新指数得分在60≤x<70这一组的是:61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
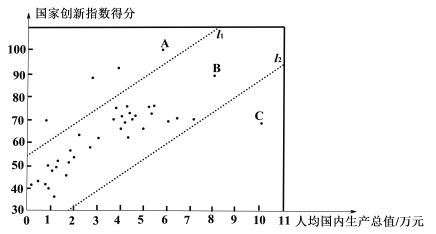
d.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第______;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线![]() 的上方.请在图中用“
的上方.请在图中用“![]() ”圈出代表中国的点;
”圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为______万美元;(结果保留一位小数)
(4)下列推断合理的是______.
①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将形状、大小完全相同的两个等腰三角形如图所示放置,点![]() 在
在![]() 边上,
边上,![]() 绕点
绕点![]() 旋转,腰
旋转,腰![]() 和底边
和底边![]() 分别交
分别交![]() 的两腰
的两腰![]() 于
于![]() 两点,若
两点,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值为( )
的最小值为( )
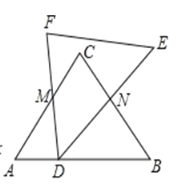
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格纸中,每一个小正方形的边长为一线段AB的两个端点都在小正方形的顶点上,请按下面的要求画图.
(1)在图1中画钝角三角形ABC,点C落在小正方形顶点上,其中△ABC有一个内角为135°,△ABC的面积为4,并直接写出∠ABC的正切值;
(2)在图1中沿小正方形网格线画一条裁剪线,沿此裁剪线将钝角三角形ABC分隔成两部分图形,按所裁剪图形的实际大小,将这两部分图形在图2中拼成一个平行四边形DEFG,要求裁成的两部分图形在拼成平行四边形时互不重叠且不留空隙,其中所拼成的平行四边形的周长为8+2![]() ,各顶点必须与小正方形的顶点重合.
,各顶点必须与小正方形的顶点重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
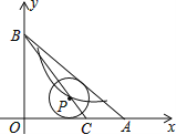
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c图象的一部分,且抛物线的对称轴为x=﹣1,那么下列说法正确的是( )
①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0.

A. ①②③④B. ②④⑤C. ②③④D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
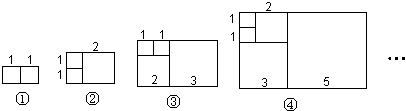
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元;
(1)求键盘和鼠标的单价各是多少元?
(2)经过与经销商洽谈,键盘打八折,鼠标打八五折.若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com