
【题目】为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元;
(1)求键盘和鼠标的单价各是多少元?
(2)经过与经销商洽谈,键盘打八折,鼠标打八五折.若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘多少个?
【答案】(1)键盘的单价为50元/个,鼠标的单价为40元/个;(2)20个.
【解析】
(1)设键盘的单价为![]() 元/个,鼠标的单价为
元/个,鼠标的单价为![]() 元/个,根据“购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元”,即可得出关于
元/个,根据“购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元”,即可得出关于![]() ,
,![]() 的二元一次方程组,解之即可得出结论;
的二元一次方程组,解之即可得出结论;
(2)设购买键盘m个,则购买鼠标(50m)个,根据总价=单价×折扣率×数量结合总费用不超过1820元,即可得出关于m的一元一次不等式,解之取其最大值即可得出结论.
解:(1)设键盘的单价为![]() 元/个,鼠标的单价为
元/个,鼠标的单价为![]() 元/个,
元/个,
根据题意得:![]() ,
,
解得:![]() .
.
答:键盘的单价为50元/个,鼠标的单价为40元/个.
(2)设购买键盘![]() 个,则购买鼠标(50﹣
个,则购买鼠标(50﹣![]() )个,
)个,
根据题意得:50×0.8m+40×0.85(50﹣m)≤1820,
解得:m≤20.
答:最多可购买键盘20个.


科目:初中数学 来源: 题型:
【题目】随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A .和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表(部分信息未给出):

根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(3)若该中学约有![]() 名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
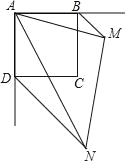
【题目】已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
(1)求证:△ABM∽△NDA;
(2)联结BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
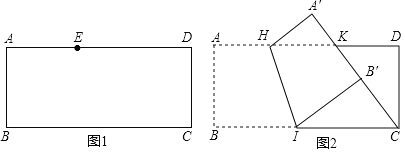
【题目】有一张矩形纸片ABCD,![]() ,
,![]() .
.
![]() 如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为
如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为![]() 点M,N分别在边AD,BC上
点M,N分别在边AD,BC上![]() ,利用直尺和圆规画出折痕
,利用直尺和圆规画出折痕![]() 不写作法,保留作图痕迹
不写作法,保留作图痕迹![]() ;
;
![]() 如图2,点K在这张矩形纸片的边AD上,
如图2,点K在这张矩形纸片的边AD上,![]() ,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点
,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点![]() ,
,![]() 处,小明认为
处,小明认为![]() 所在直线恰好经过点D,他的判断是否正确,请说明理由.
所在直线恰好经过点D,他的判断是否正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
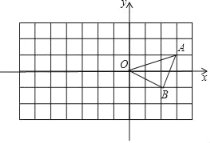
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示,解答问题:
(1)请按要求对△OAB作变换:以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA′B′.
(2)写出点A′的坐标;
(3)求△OA′B'的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
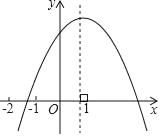
【题目】如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为经过点(1,0)且垂直于x轴的直线.给出四个结论:①abc>0;②当x>1时,y随x的增大面减小;③4a﹣2b+c>0;④3a+c>0.其中正确的结论是_____(写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
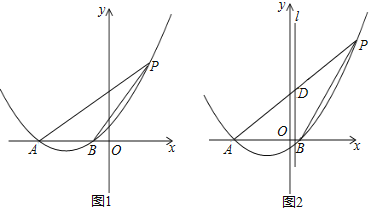
【题目】已知抛物线![]() ,其中
,其中![]() ,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移
,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移![]() 个单位长度后,与x轴交于点A、B,
个单位长度后,与x轴交于点A、B,![]() 在B的左侧
在B的左侧![]() ,如图1,P为平移后的抛物线上位于第一象限内的一点
,如图1,P为平移后的抛物线上位于第一象限内的一点
![]() 点A的坐标为______;
点A的坐标为______;
![]() 若点P的横坐标为
若点P的横坐标为![]() ,求出当m为何值时
,求出当m为何值时![]() 的面积最大,并求出这个最大值;
的面积最大,并求出这个最大值;
![]() 如图2,AP交l于点D,当D为AP的中点时,求证:
如图2,AP交l于点D,当D为AP的中点时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
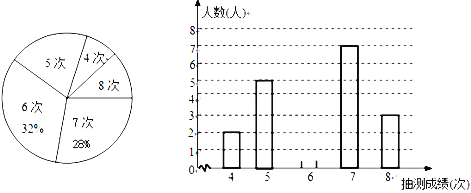
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
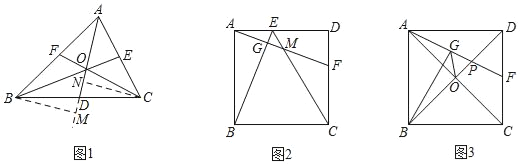
【题目】(探索发现)如图1,△ABC中,点D,E,F分别在边BC,AC,AB上,且AD,BE,CF相交于同一点O.用”S”表示三角形的面积,有S△ABD:S△ACD=BD:CD,这一结论可通过以下推理得到:过点B作BM⊥AD,交AD延长线于点M,过点C作CN⊥AD于点N,可得S△ABD:S△ACD=![]() ,又可证△BDM~△CDN,∴BM:CN=BD:CD,∴S△ABD:S△ACD=BD:CD.由此可得S△BAO:S△BCO= ;S△CAO:S△CBO= ;若D,E,F分别是BC,AC,AB的中点,则S△BFO:S△ABC= .
,又可证△BDM~△CDN,∴BM:CN=BD:CD,∴S△ABD:S△ACD=BD:CD.由此可得S△BAO:S△BCO= ;S△CAO:S△CBO= ;若D,E,F分别是BC,AC,AB的中点,则S△BFO:S△ABC= .
(灵活运用)如图2,正方形ABCD中,点E,F分别在边AD,CD上,连接AF,BE和CE,AF分别交BE,CE于点G,M.
(1)若AE=DF.判断AF与BE的位置关系与数量关系,并说明理由;
(2)若点E,F分别是边AD,CD的中点,且AB=4.则四边形EMFD的面积是 .
(拓展应用)如图3,正方形ABCD中,AB=4,对角线AC,BD相交于点O.点F是边CD的中点.AF与BD相交于点P,BG⊥AF于点G,连接OG,请直接写出S△OGP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com