
【题目】如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
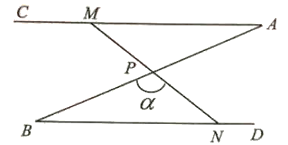
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
【答案】(1)见解析;(2)30°;(3)![]()
【解析】
(1)由P为AB的中点,可得PA=PB,再由已知中∠A=∠B=30°,对顶角∠APM=∠BPN,根据ASA即可判定△APM≌△BPN;
(2)由(1)中结论可知PM=PN,即MN=2PN,由已知MN=2BN,可得BN=PN,根据等边对等角,即α=∠B=30°;
(3)当α=60°时,由∠B=30°,可知MN⊥BD,此时BP的中点为△BPN的外心,当α=90°时,由∠B=30°,此时BN的中点为△BPN的外心,根据三角形中位线定理可得△BPN的外心运动路线的长度为PN的一半,即为![]() .
.
(1)证明:∵P是AB的中点,∴PA=PB , 在△APM和△BPN中, 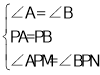
∴△APM≌△BPN(ASA)
(2)解:由(1)得:△APM≌△BPN , ∴PM=PN , ∴MN=2PN , ∵MN=2BN , ∴BN=PN , ∴α=∠B=30°
(3)解: ![]()


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
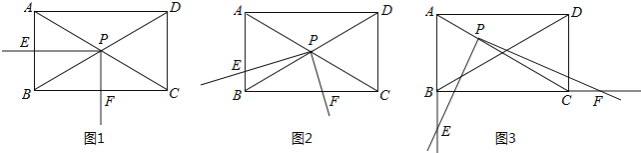
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
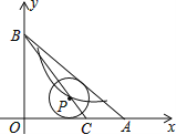
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,单价30元,试销中发现这种商品每天的销售量夕(件)与每件的销售价![]() (元)满足关系:
(元)满足关系:![]() =100-2
=100-2![]() .若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
.若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .
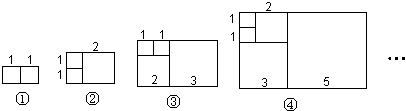
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x﹣6与x轴、y轴分别交于B、C两点,A是以D(0,2)为圆心,2为半径的圆上一动点,连结AC、AB,则△ABC面积的最小值是( )
x﹣6与x轴、y轴分别交于B、C两点,A是以D(0,2)为圆心,2为半径的圆上一动点,连结AC、AB,则△ABC面积的最小值是( )
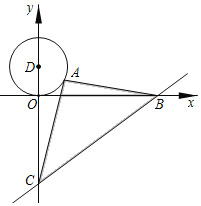
A. 26B. 24C. 22D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+2的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
(1)请求出二次函数的解析式;
(2)若点M(m,n)在抛物线的对称轴上,且AM平分∠OAC,求n的值.
(3)若P是线段AB上的一个动点(不与A、B重合),过P作PQ∥AC,与AB上方的抛物线交于点Q,与x轴交于点H,试问:是否存在这样的点Q,使PH=2QH?若存在,请直接出点Q的坐标;若不存在,请说明理由.
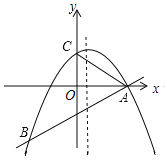
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,在△ABC内一点P,已知∠1=∠2=∠3,将△BCP以直线PC为对称轴翻折,使点B与点D重合,PD与AB交于点E,连结AD,将△APD的面积记为S1,将△BPE的面积记为S2,则![]() 的值为_____.
的值为_____.
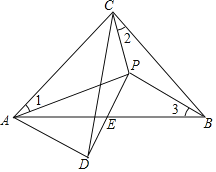
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.

(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形ADBC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com