
【题目】如图,已知ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=![]() ,求CF的长.
,求CF的长.
【答案】(1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=![]() ,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠ADE=∠DEC,
又∵∠AFC=∠DEC,∴∠AFC=∠ADE,
∴DE∥FC,
∴四边形DECF是平行四边形;
(2)过点D作DH⊥BC于点H,如图所示.
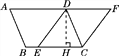
∵四边形ABCD是平行四边形,
∴∠BCD=∠A,AB=CD=13,
又∵tan A=![]() =tan∠DCH=
=tan∠DCH=![]() ,
,
∴DH=12,CH=5,
∵DF=14,∴CE=14,
∴EH=9,
∴DE=![]() =15,
=15,
∴CF=DE=15.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
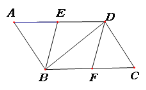
【题目】如图,在平行四边形ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)当△ABD满足什么条件时,四边形EBFD是菱形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都至西安的高速铁路(简称西成高铁)全线正式运营,至此,从成都至西安有两条铁路线可选择:一条是普通列车行驶线路(宝成线),全长825千米;另一条是高速列车行驶线路(西成高铁),全长660千米,高速列车在西成高铁线上行驶的平均速度是普通列车在宝成线上行驶的平均速度的3倍,乘坐普通列车从成都至西安比乘坐高速列车从成都至西安多用11小时,则高速列车在西成高铁上行驶的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两江新区某小学每年的六一儿童节都会举办不同主题色的童装盛会,记录孩子们成长的印记这种活动让商家们看到了新的商机,某网店获悉今年的主题色是梦幻紫色,在六一节前购进梦幻紫色系列的A、B两款童装共86件,其中A款童装120元每件.B款童装80元每件,共用去资金8480元.
(1)求此网店购A、B两款童装各多少件?
(2)六一儿童节的童装盛会反响非常好,引起社会上的童爸童妈们的高度关注,将这两款童装再次推向了热销,此网店决定再次购进A、B两款童装,数量与上次相同,购进时,发现A款童装的进价上涨了![]() %,B款童装的进价下降了之
%,B款童装的进价下降了之![]() %,总价不超过9050元,求
%,总价不超过9050元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
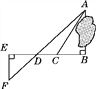
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
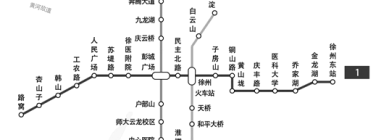
【题目】徐州地铁1号线,西起杏山子大道,止于高铁徐州东站,共设18座站点,18座站点如下所示.徐州轨道交通试运营期间,小苏从苏堤路站开始乘坐地铁,在地铁各站点做志愿者服务,到![]() 站下车时,本次志愿者服务活动结束,约定向徐州东站站方向(即箭头方向)为正,当天的乘车记录如下(单位:站):
站下车时,本次志愿者服务活动结束,约定向徐州东站站方向(即箭头方向)为正,当天的乘车记录如下(单位:站):![]() ,-2,-6,
,-2,-6,![]() 8,
8,![]() 3,-4,-9,
3,-4,-9,![]() 8.
8.

(1)请通过计算说明![]() 站是哪一站?
站是哪一站?
(2)如果相邻两站之间的距离为![]() 千米,求这次小苏志愿服务期间乘坐地铁行进的总路程是多少千米?
千米,求这次小苏志愿服务期间乘坐地铁行进的总路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知动点P(t-6,![]() )在定直线l1上运动.
)在定直线l1上运动.

(1) 求直线l1的函数解析式;
(2) 如图1,l1与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称,过点P作y轴的平行线,交x轴于点M,交直线BC于点Q;
① 若△PQB的面积为3,求点M的坐标;
② 如图2,连接BM.若∠BMP=∠BAC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+bx﹣1.
(1)求证:无论b取什么值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点.
(2)若两点P(﹣3,m)和Q(1,m)在该函数图象上.
①求b、m的值;
②将二次函数图象向上平移多少单位长度后,得到的函数图象与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com