
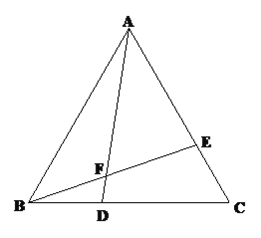
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,且BD=CE,AD与BE相交于点F.
(1)求证:△ABD≌△BCE
(2)求证: ![]()
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:
(1) 要证△ABD≌△BCE,利用△ABC是等边三角形可以得到,AB=BC,∠ABC=∠BCA. 在这种情况下观察图形可知,在待证明的两个三角形中已经获得一组对应边相等和一组对应角相等,再根据已知条件BD=CE,根据SAS即可证明这两个三角形全等.
(2) 观察待证明的等式形式可知,AE应为BE和EF的比例中项. 将待证明的等式改写为比例式后,利用“三点定形法”可以找到一组合适的相似三角形△EBA与△EAF. 观察这两个三角形发现:这两个三角形有一组对应角为公共角;对于另一组对应角∠EBA与∠EAF而言,可以通过第(1)问中的全等三角形和△ABC的性质证明其相等. 利用相似三角形的判定定理即可获得这组三角形相似,进而证明等式成立.
试题解析:
(1) ∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠BCA,即∠ABD=∠BCE,
∵在△ABD与△BCE中:
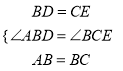 ,
,
∴△ABD≌△BCE (SAS).
(2) ∵△ABC是等边三角形,
∴∠ABC=∠BAC,
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠ABC-∠CBE =∠BAC-∠BAD,
∴∠EBA=∠CAD,即∠EBA=∠EAF,
∵在△EBA与△EAF中:
∠AEB=∠FEA (公共角),∠EBA=∠EAF,
∴△EBA∽△EAF,
∴![]() ,
,
即AE2=BE·EF.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图①,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地路程y(千米)与行驶时间x(小时)的函数关系图象.
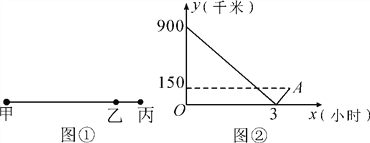
(1)填空:甲、丙两地距离_______千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为备战2011年4月11日在绍兴举行的第三届全国皮划艇马拉松赛,甲、乙运动员进行了艰苦的训练,他们在相同条件下各10次划艇成绩的平均数相同,方差分别为0.23,0.20,则成绩较为稳定的是(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
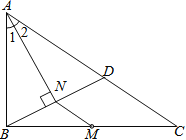
(1)求证:BN=DN;
(2)求△ABC的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com