
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上).给出以下判断:
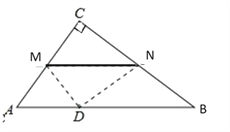
①当MN∥AB时,CM=AM;
②当四边形CMDN为矩形时,AC=BC;
③当点D为AB的中点时,∠CMN=∠B;
④当∠CMN=∠B时,点D为AB的中点;
其中正确的是__.(把所有正确结论序号都填在横线上).
【答案】①③④
【解析】①∵MN∥AB,
∴∠CMN=∠CAB,∠NMD=∠MDA,
由翻折变换的性质可知,∠CMN=∠DMN,CM=DM,
∴∠CAB=∠MDA,
∴AM=DM,
∴CM=AM,故①正确;
②根据折叠的性质得到CE=DE,矩形CEDF是正方形,
又任意一个直角三角形都有一个内接正方形满足题意,
故②错误;
③当点D是AB的中点时,∠CMN=∠B,
理由如下:如图2,连接CD,与EF交于点Q,
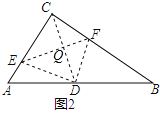
∵CD是Rt△ABC的中线,
∴CD=DB=![]() AB,
AB,
∴∠DCB=∠B,
由轴对称的性质可知,∠CQF=∠DQF=90°,
∴∠DCB+∠CFE=90°,
∵∠B+∠A=90°,
∴∠CFE=∠A,
又∵∠C=∠C,
∴△CEF∽△CBA;
∴∠CMN=∠B,
故③正确;
④∵当∠CMN=∠B时
∴△CEF与△ABC相似,
∴∠EFD=∠CAB,∠EDF=∠ECF=90°,
∴C,E,D,F四点共圆,
∴∠ACD=∠EFD,
∴∠ACD=∠A,
∴AD=CD,同理CD=BD,
∴点D为AB的中点,故④正确,
故答案为:①③④.
点睛: 本题是几何综合题,考查了几何图形折叠问题,勾股定理和全等三角形的判定与性质,难度适中,运用分类讨论及数形结合思想是解题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=25,AB=12,点E、F分别是AD、BC上的点,且DE=CF=9,连接EF、DF、AF.取AF的中点为G,连接BG,将△BFG沿BC方向平移,当点F到达点C时停止平移,然后将△GFB绕C点顺时针旋转α(0°<α<90°),得到△B1CG1(点G的对应点为G1,点B的对应点为B1),在旋转过程中,直线B1G1与直线EF、FD分别相交M、N,当△FMN是等腰三角形,且FM=FN时,线段DN的长为 .
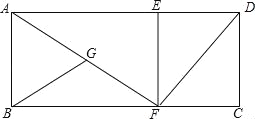
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
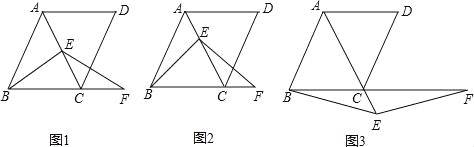
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下面证明过程中的推理依据:
已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.求证:∠1=∠2
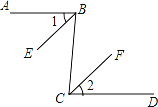
证明:∵AB∥CD (__________)
∴∠ABC=∠BCD(__________)
∵BE平分∠ABC,CF平分∠BCD (__________)
∴∠1=![]() ∠ ______ ,(__________)
∠ ______ ,(__________)
∠2=![]() ∠ ______ .(__________)
∠ ______ .(__________)
∴∠1=∠2.(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阜阳市出租车收费标准是:起步价5元,可乘3千米;超过3千米,超过部分每千米2.4元.
(1)若某人乘坐了x(x>3)千米的路程,则他应支付的费用是多少?
(2)若某人乘坐的路程为10千米,那么他应支付的费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】M(1,a)是一次函数y=3x+2与反比例函数![]() 图象的公共点,将一次函数y=3x+2的图象向下平移4个单位得到的解析式为y=kx+b
图象的公共点,将一次函数y=3x+2的图象向下平移4个单位得到的解析式为y=kx+b
(1)求y=kx+b和![]() 的解析式.
的解析式.
(2)若![]() 为双曲线
为双曲线![]() 上三点,且
上三点,且![]() ,请直接写出
,请直接写出![]() 大小关系;
大小关系;
(3)画出图象,观察图象直接写出不等式kx+b>![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com